Construct Triangle from Altitude, Median and Inradius
What Might This Be About?
Problem
Construct $\Delta ABC,$ given $m_a,$ $h_a,$ and the inradius $r.$
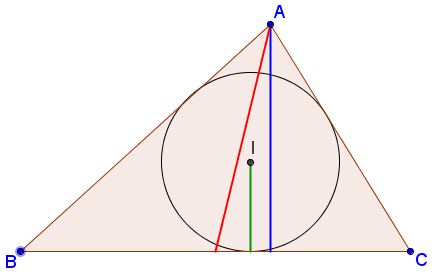
Analysis
A construction of a triangle from $h_a,$ $m_a$ and $r$ is clear if the length $x$ from $E$ to $A$ can be found. A straightforward way to calculate $x$ is by means of analytic geometry.
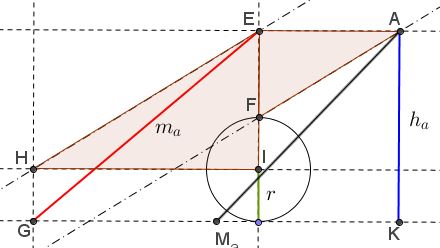
If we consider $A$ as a point with coordinates $(x_0, y_0),$ $y_0 = h - r$ (the origin being in the center of the incircle), then the intersection of the line given by $x_0x + y_0 y = r^2$ with the circle $x^2 + y^2 = r^2$ gives the points of tangency, say $(x_1, y_1)$ and $(x_2, y_2).$ Then the two tangents have the equations $x_1x + y_1y = r^2$ and $x_2x + y_2 y = r^2$ (see, e.g., a href="https://www.cut-the-knot.org/Generalization/JoachimsthalsNotations.shtml">Joachimsthal's Notations.)
If these tangents are intersected with the line $y = - r$ we get the coordinates of $B$ and $C.$ One just has to solve quadratic equations. While the expressions for the $x_i$ and $y_i$ are rather involved, the expression for the distance $d$ (half length of $BC)$ turns out to be very simple:
$\displaystyle d = \frac{rx_0}{r+x_0}.$
The condition
$(d + x)^2 + h_a^2=m_a^2$
then determines $x$ and one finds
$\displaystyle x = \frac{h-r}{h-2r}\sqrt{m_a^2-h_a^2}.$ This means that the two triangles $IHE$ and $EAF$ are similar, so that $AF\parallel EH;$ and this suggests the construction.
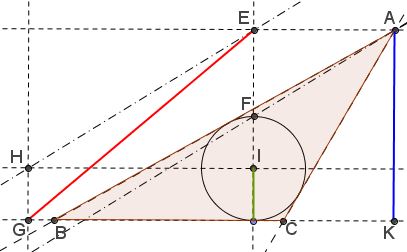
Construction
Step 1: Start with two parallel lines at distance $h_a$ from each other.
Step 2: Draw a circle of radius $r$ tangent to one of the parallels.
Step 3: Draw the perpendicular through the center of the circle to obtain points $E$ and $F.$
Step 4: Draw a segment of length $m_a$ from point $E$ to get point $G$ (this may produce two distinct points.)
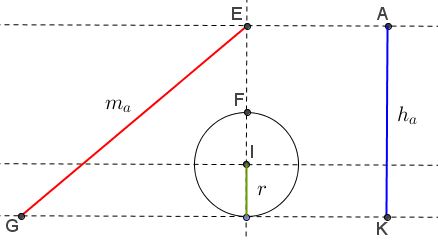
Step 5: Find point $H$ at distance $r$ from $G.$
Step 6: Draw the parallel to $HE$ through point $F.$ This line intersects the other parallel in vertex $A.$
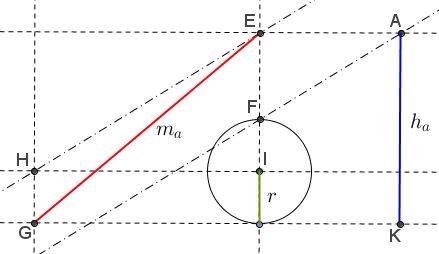
Step 7: From $A$ construct the tangents to the circle to find vertices $B$ and $C.$
Acknowledgment
The construction is due to Prof. Dr. René Sperb.
![]()
|Contact| |Front page| |Contents| |Geometry| |Triangle constructions|
Copyright © 1996-2018 Alexander Bogomolny73576477
