Construct Triangle by Angle Bisector, Altitude, and Side
What Might This Be About?
Problem
Construct $\Delta ABC,$ given $h_a,$ $l_a,$ and $a.$
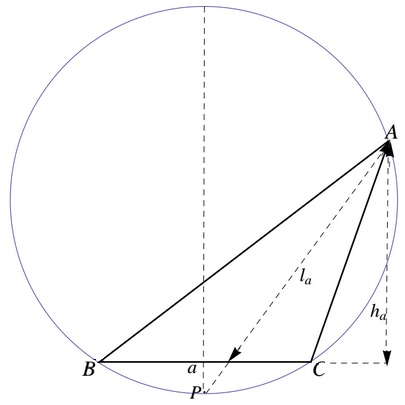
Analysis

It is sufficient to determine the circumcircle of $\Delta ABC.$
Construction
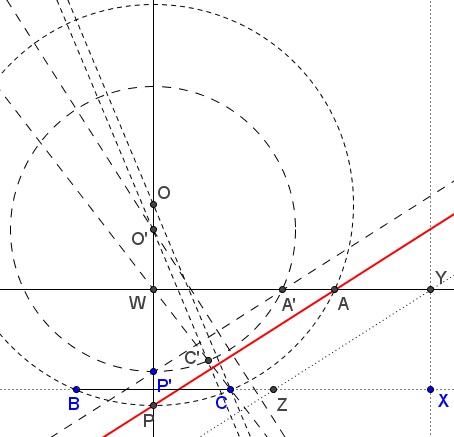
Step 1: First determine the direction of the angle bisector relative to the line $BC.$ To this end, construct right $\Delta XYZ,$ with $XY=h_a$ and $YZ=l_a.$ $YZ$ defines the required direction. Draw $YW\parallel BC,$ with $W$ on t he perpendiclar bisector of $BC.$
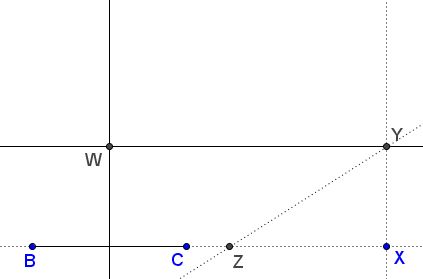
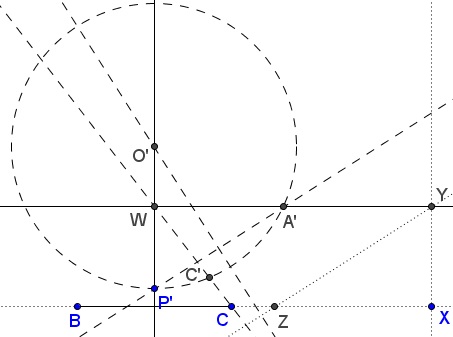
Step 2: Select an arbitary point $P'$ on the perpendicular bisector of $BC$ and find point $P'$ on $YW$ such that $A'P'\parallel YZ.$
Let $O'$ be the intersection of the perpendicular bisectors of $BC$ and $A'P'.$ Consider circle $(O')$ with center $O'$ through $A'$ and $P'.$ If it also passes through $B$ and $C$ the problem is solved: $A=A'.$

Step 3: Let $C'$ be the intersection of $(O')$ and $CW.$
Step 4: Draw $CO\parallel C'O',$ with $O$ on the perpendicular bisector of $BC.$
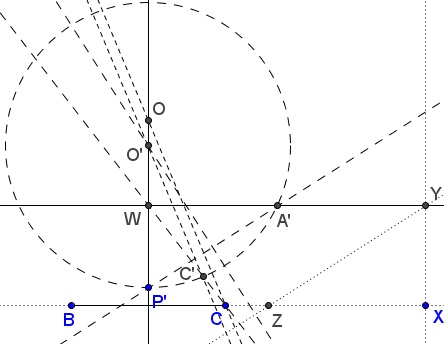
Step 5: Circle $(O)$ with center $O$ through $B$ and $C$ cuts $YW$ in $A,$ the missing vertex of the sought triangle.
Proof
Note that the circles $(O')$ obtained due to various selections of $P'$ are homothetic at $W$ so that all lines $C'O'$ are parallel. Since $P'$ is always on the perpendicular bisector of $BC$ and thus is the lowest point of $(O'),$ for the circle $(O)$ through $B$ and $C,$ $P$ is the mid point of the arc $BC,$ making $AP$ the bisector of $\angle ABC.$ Naturally, the part of $AP$ between the parallels $BC$ and $YW$ equals $YZ=l_a.$
Acknowledgment
The construction is due to Prof. Dr. René Sperb.
![]()
|Contact| |Front page| |Contents| |Geometry| |Triangle constructions|
Copyright © 1996-2018 Alexander Bogomolny73579322
