Construct Triangle from Angle, Inradius, and Altitude
What Might This Be About?
Problem
Construct $\Delta ABC,$ given angle $A=\angle BAC,$ the inradius $r,$ and the altitude $h_a.$
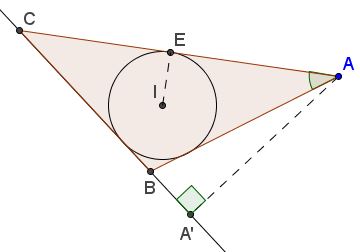
Analysis
The sideline $BC$ of $\Delta ABC$ serves as the common tangent to the incircle $(I)$ and circle $C(A,h_{a})$ centered at $A,$with $h_a$ as the radius.
Construction
Start at the vertex $A$ with the given angle $A$ and then inscribe a circle $(I)$ of radius $r.$
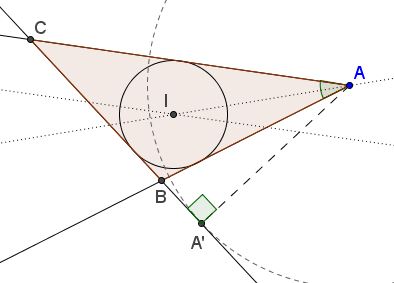
Draw $C(A,h_{a})$ and find common external tangents for $(I)$ and $C(A,h_{a}).$ Choose one of the two. It intersects the sides of the angle $A$ in points $B$ and $C.$
The tangent may not exist if circle $(I)$ lies entirely within $C(A,h_{a}).$ If the given altitude is smaller than the inradius, the construction leads to a triangle for which $(I)$ is an excircle. The same happens if one chooses the inner instead of external common tangent of the two circles.
Acknowledgment
The construction is due to Prof. Dr. René Sperb.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73573586
