Conics in Triangle
What Might This Be About?
Problem
Three conics each with a focus at a vertex of a triangle and the directrix - the side opposite the focus - cut the sides of the triangle in six points that lie on a conic.
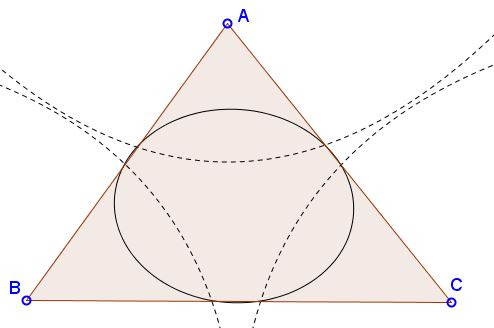
Solution
Denote the intersections of the conics with the side of $\Delta ABC$ as shown below. Drop the perpendiculars from the points of intersections to the corresponding directrices:
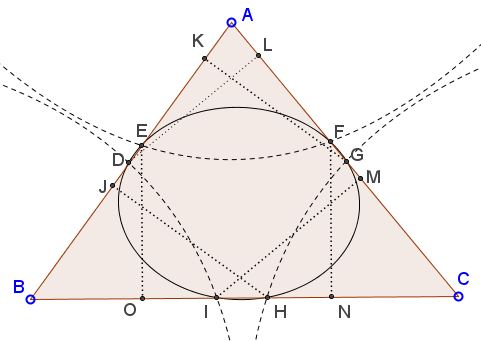
Let the eccentricities of the three conics be $\alpha,$ $\beta,$ and $\gamma.$ By the definition,
$ AF = \alpha FN,\space AE = \alpha EO,\\ BD = \beta DL,\space BI = \beta IM,\\ CH = \gamma HJ,\space CG = \gamma GK. $
Let $AA',$ $BB',$ $CC'$ be the altitudes of $\Delta ABC.$ There are several triples of similar (right) triangles, e.g., $\Delta AEL\sim \Delta AGK \sim \Delta ABB'.$ By similarity,
$ \displaystyle \frac{CF}{AC} = \frac{FN}{AA'}=\frac{AF}{\alpha\cdot AA'},\\ \displaystyle \frac{AC}{AG} = \frac{CC'}{GK}=\frac{\gamma\cdot CC'}{CG},\\ \displaystyle \frac{AD}{AB} = \frac{DL}{BB'}=\frac{BD}{\beta BB'},\\ \displaystyle \frac{AB}{BE} = \frac{AA'}{EO}=\frac{\alpha AA'}{AE},\\ \displaystyle \frac{BH}{BC} = \frac{HJ}{CC'}=\frac{CH}{\gamma CC'},\\ \displaystyle \frac{BC}{CI} = \frac{BB'}{IM}=\frac{\beta BB'}{BI}.\\ $
The product of the six amounts to
$ \displaystyle\frac{CF\cdot AD\cdot BH}{AG\cdot BE\cdot CI}=\frac{AF\cdot BD\cdot CH}{CG\cdot AE\cdot BI} $
or,
$ CG\cdot CF\cdot AE\cdot AD\cdot BI\cdot BH = CH\cdot CI\cdot BD\cdot BE\cdot AF\cdot AG, $
which, by Carnot's theorem for conics, exactly means that the six points $D,E,F,G,H,I$ lie on a conic.
Acknowledgment
The statement and the solution were posted by Emmanuel Antonio José Garcíaat the CutTheKnotMath facebook page for the three conics being parabolas and at the Yahoo Advanced Plane Geometry Group where Barry Wolk observed that eccentricities of the three conics may be arbitrary. Above, I adapted Antonio's original proof taking into account Barry's observation.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73564451
