Symmetry in an Asymmetric Configuration
What is this about?
Problem
Through point $E$ on the diagonal $AC$ of square $ABCD$ two lines $FH$ and $GI$ parallel to the sides of the square are drawn, as shown below.
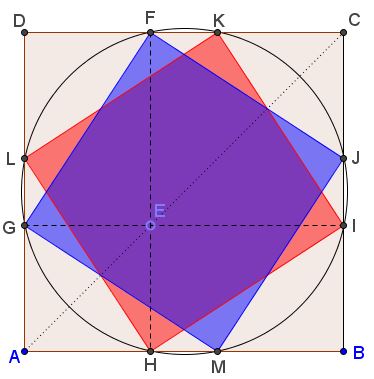
Prove that
Points $F,G,H,I$ lie on a circle that cuts the sides of the square in four additional points $J,K,L,M,$
Quadrilaterals $FGMJ$ and $HIKL$ are squares.
Solution
Let $O$ be the center of square $ABCD.$ Denote $r_{O}$ the counterclockwise rotation through $90^{\circ}$ around $O.$ This rotation takes $AH$ to $BI$ because $AH=AG=BI.$ So that $r_{O}(H)=I.$ Similarly, $r_{O}(I)=F,$ $r_{O}(F)=G,$ so that the four points $F,G,H,I$ do lie on a circle centered at $O.$
Since circle $(FGHI)$ is centered at the center of the square, the additional points $J,K,L,M$ where it meets the sides, together with $F,G,H,I,$ satisfy certain symmetry conditions. For example, $CK=CJ=BI.$ From here, the quadrilaterals $FGMJ$ and $HIKL$ are indeed squares.
The configuration of square $ABCD$ and the eight additional points on its sides possesses all the symmetries of the square: rotation by $90^{\circ}$ and reflections in the diagonals and the midlines of the square. With the introduction of more cross points (like in the diagram below), it also provides nice practice for computing segment ratios.
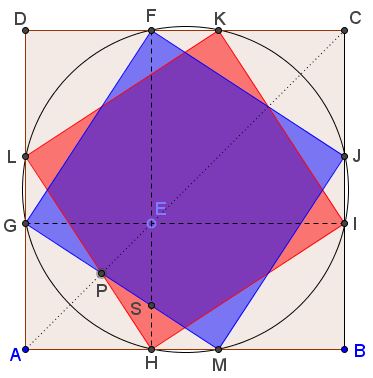
For example, $\displaystyle\frac{SE}{HS},\,\frac{MP}{GP},\,\frac{PS}{GP},\,\frac{AP}{EP}$ which are equal when $DGEF$ is a Golden Rectangle, the common value being the Golden Ratio.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581628
