Red and Pink Areas
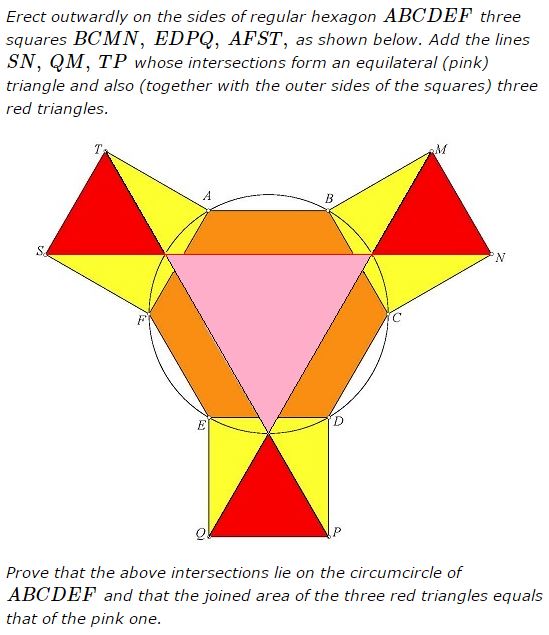
Problem
Solution 1
Let $A=2,\,$ $F=1+i\sqrt{3},\,$ $E=-1+i\sqrt{3},\,$ $D=-2,\,$ $C=-1-i\sqrt{3},\,$ and $B=1-i\sqrt{3}.\,$ Since $\displaystyle\frac{S-F}{A-F}=i,\,$ we get $S=1+\sqrt{3}+i(1+\sqrt{3})\,$ and, since $A+S=T+F,\,$ $T=2+\sqrt{3}+i.$
Similarly, $\displaystyle\frac{M-B}{C-b}=i\,$ implies $M=1-i(2+\sqrt{3})\,$ and from $M+C=B+N\,$ we get $N=-1-i(2+\sqrt{3}).$
Clearly, the lines $AB\,$ and $SN\,$ have the slope $\sqrt{3},\,$ such that $AB\parallel SN.\,$ The midpoint of the minor arc $AF\,$ is $\sqrt{3}+i\,$ and the midpoint of the minor arc $BC\,$ is $-2i.\,$ We deduce easily that the two midpoints are on the line $SN.\,$ Further, the two triangles are equilateral. Similarly, the other red triangles are also equilateral. The side of the pink triangle is $|\sqrt{3}+3i|=2\sqrt{3}\,$ and, since the common side lengths of the red triangles and and the hexagon is $2,\,$ the conclusion follows.
Solution 2
I assume that the fact that the lines $NS,\,$ $MQ,\,$ and $PT\,$ meet at the $60^{\circ}\,$ angles. Consider the line through the center $O\,$ of the hexagon perpendicular to $MN.\,$
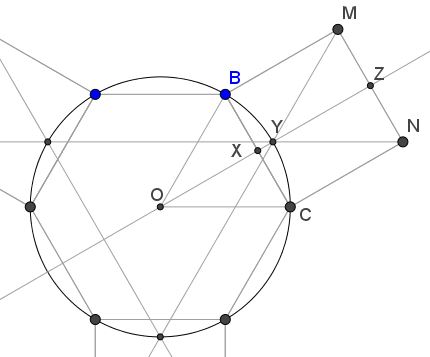
This line meets $BC\,$ at $X\,$ and $MN\,$ at $Z.\,$ Due to the symmetry of the configuration, it also passes through the intersection of $NS\,$ and $MQ\,$ which is denoted $Y.\,$ Now, $OX+XZ=OY+YZ,\,$ such that $OY=XZ+(OX-YZ)=XZ.\,$ But $OX=YZ,\,$ as both are the altitudes in equal equilateral triangles. Hence, $OY=XZ,\,$ implying that $Y\,$ lies on the circumcircle of $ABCDEF.$
With a little trigonometry, the side of the pink triangle equals $\sqrt{3}\,$ that of the red ones such that its area is $3\,$ times as large.
Acknowledgment
The problem has been kindly posted by Tran Quang Hung at the CuTheKnotMath facebook page. Solution 1 is by Leo Giugiuc.
Originally, the pink triangle has been green. However, this is a well-known fact that about 8% of all men and 0.5% of all women are incapable of telling red from green. To make the drawing more accessible I painted the green triangle pink.
|Contact| |front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574072
