Three Circles and Area

Source

The following problem, due to Miguel Ochoa Sanchez, has been posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.

Three Circles and Area - the original

Problem

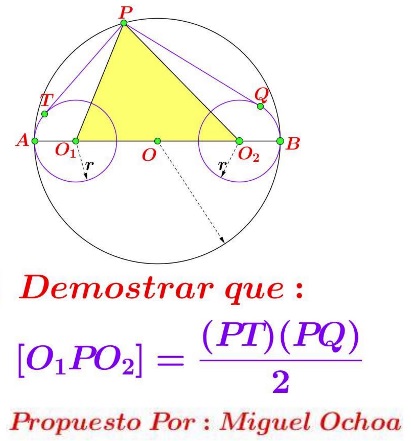
Points $O_1$ and $O_2$ lie on the diameter $AB$ of circle $(O).$ Circle $O_1(r)$ is tangent to $(O)$ at $A,\;$ $O_2(r)$ is tangent to $(O)$ at $B,\;$ for some $r\gt 0.$ $P\;$ is on $(O);$ $PT$ is tangent to $O_1(r),\;$ $PQ$ is tangent to $O_2(r).$

Prove that $\displaystyle\frac{PT\cdot PQ}{2}=[\Delta O_1PO_2],$

where $[F]$ denotes the area of shape $F.$

Solution

Assume $(O)$ is described by the equation $x^2+y^2=1;$ $A=(-1,0),$ $B=(1,0),$ $P=(\cos t,\sin t),$ with $t\in(0,\pi ).\;$ Obviously, $O_1=(-1+r,0)\;$ and $O_2=(1-r,0). From here

$[\Delta O_1PO_2]=\displaystyle\frac{1}{2}O_1O_2\cdot\sin t=\frac{2-2r}{2}\sin t=(1-r)\sin t.$

On the other hand, by the Pythagorean theorem in triangles $PO_1T$ and $PCO_1,$

Three Circles and Area - solution

or the Power of a Point theorem,

$O_1P^2-r^2=PT^2=2(1-r)(1+\cos t),$ or $PT=\sqrt{2(1-r)(1+\cos t)}.\;$ Similarly, $PQ=\sqrt{2(1-r)(1-\cos t)}.\;$ It thus follows that $PR\cdot PQ=2(1-r)\sin t,$

as expected.

71948530