Tangent Curiosity in Equilateral Triangle
What Might This Be About?
Problem
In an equilateral triangle $ABC,$ two circles are tangent to the base $BC,$ the circumcircle $(ABC)$ and to each other. $AP$ is tangent to one, $AQ$ to the other. $M$ and $N$ are their respective points of tangency with the base.
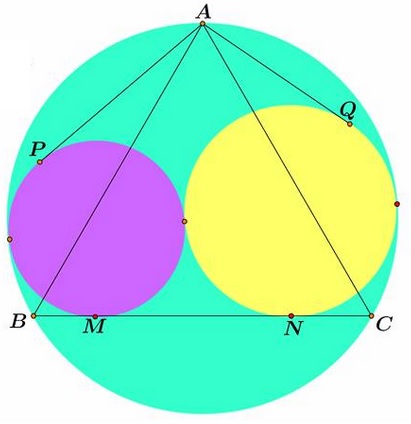
Prove that $AP+AQ=2MN.$
Solution 1
As we shall see, the requirement that the two circles are tangent to each other is a red herring: the required identity holds even if they are not. The purpose of the applet above was to suggest an even stronger result.
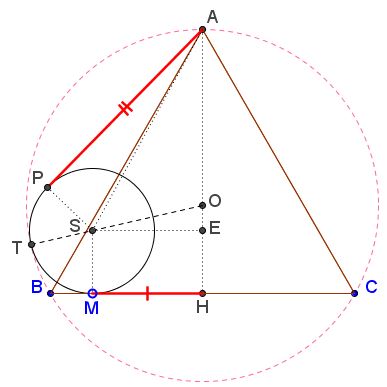
The proof is analytic. Let $B=(-3,0),$ $C=(3,0),$ $A(0,3\sqrt{3}).$ This makes the side length of $\Delta ABC$ $6,$ the circumradius $AO=R=2\sqrt{3}$ and the inradius $OH=r=\sqrt{3}.$ $H$ the midpoint of the base is at the origin. We focus on the left circle as shown.
There is a good deal of right triangles that, through a repeated use of the Pythagorean theorem, lead to the relation
$AP=2MH$
which clearly solves the problem because a similar identity holds for the right triangle. (Note that in fact two configurations are possible: one shown above, the other for the case where $S$ is above $O.$ We stick with the one shown; the other submits to an only slightly different treatment.)
So, $S$ is the center of the left circle whose radius is denoted $s,$ and $MH=a.$
In $\Delta EOS,$ $EO^{2}+ES^{2}=OS^{2}.$ In other words, $a^{2}+(r-s)^{2}=(R-s)^{2}$ which leads to the relation $\displaystyle s=\frac{9-a^{2}}{2\sqrt{3}}.$
In $\Delta APS,$ $AP^{2}+PS^{2}=AS^{2}.$ Since $\displaystyle AS^{2}=(a-0)^{2}+(s-3\sqrt{3})^{2}=a^{2}+\frac{(9+a^{2})^{2}}{12}$ and $\displaystyle s^{2}=\frac{(9-a^{2})^{2}}{12},$
$\displaystyle AP^{2}= a^2 + \frac{(9+a)^{2}}{12} - \frac{(9-a)^{2}}{12} = a^{2}+\frac{18\cdot 2a^{2}}{12}=4a^{2}.$
It follows that $AP=2a=2MH,$ as promised. For the second (right) circle, we similarly get $AQ=2HN,$ so that for the two of them
$AP+AQ=2MH+2HN=2(MH+HN)=2MN.$
Solution 2
This solution too depends on a
Lemma
Two circles are tangent internally at point $T.$ From points $D$ and $G$ on the big circle, tangents $DE$ and $GF$ are drawn to the small one.
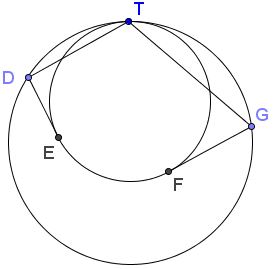
Then $\displaystyle\frac{DT}{GT}=\frac{DE}{GF}.$
Proof of Lemma
Let $D'$ and $G'$ be the intersections of $TD$ and $TG,$ respectively, with the small circles. Then, a homothety from $T,$ $\displaystyle\frac{D'T}{DT}=\frac{G'T}{GT}=t,$ where $t$ is the raio od the radii of the two circles.
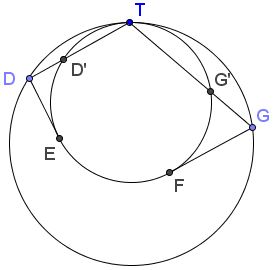
By the Power of a Point Theorem,
$GF^{2}=GT\cdot GG'=GT\cdot (GT-G'T)=GT^{2}(1-t).$
Similarly, $DE^{2}=DT\cdot DD'=DT\cdot (DT-D'T)=DT^{2}(1-t).\space$ This proves the lemma.
Proof of Statement
Introduce the notations as shown below.
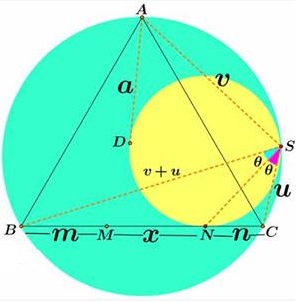
By van Schooten's theorem, $BS=AS+CS,$ or $BS=u+v.$ By Lemma, $\displaystyle\frac{a}{n}=\frac{v}{u},$ such that also $\displaystyle\frac{a+n}{n}=\frac{u+v}{u}=\frac{m+x}{n}.$ The latter stems from a property of a circle inscribed into a circular segment and a property of angle bisectors.
It follows that $AQ = a = m+x-n,$ where $x=MN.$ Similarly, $AP=n+x-m,$ so that $AP+AQ=2x=2MN.$
Acknowledgment
This problem has been posted by Miguel Ochoa Sanchez (Peru) at the CutTheKnotMath facebook page. A solution by Leo Giugiuc (Romania) followed almost immediately. Leo also suggested that the two circles did not need to be tangent to each other. The solution above follows in Leo's footsteps.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581504
