Shifted by the Inradius Tangent Collinearities

What Might This Be About?

Problem

In $\Delta ABC,$ $G$ (on $AC$) and $F$ (on $AB$) are the points of tangency of the excircle opposite $C.$ $GK\perp AC,$ $FM\perp AB,$ $GK=FM=r,$ where $r$ is the inradius of $\Delta ABC.$

Shifted by the Inradius Tangent Collinearities - problem

Prove that $B,$ $M,$ $K$ are collinear.

Solution

Let, as shown, $I$ be the incenter of $\Delta ABC$ and $J$ the point of tangency of the incircle with $AB.$ As is well known, $AF=BJ=p-b,$ where $p$ is the semiperimeter of $\Delta ABC,$ $\displaystyle p=\frac{a+b+c}{2},$ $a,b,c$ being the side lengths of the triangle.

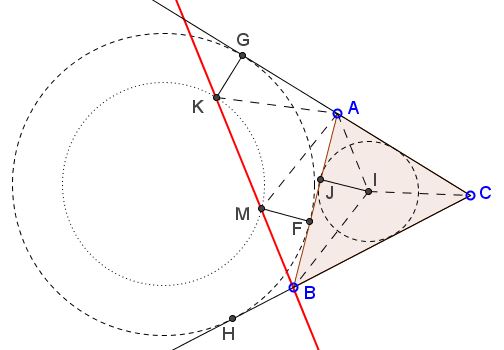
Shifted by the Inradius Tangent Collinearities - solution

This makes $AMBI$ a parallelogram. It follows that

$\begin{align}\displaystyle \angle BMF &= 180^{\circ} -90^{\circ} -\frac{\angle BAC}{2}= 90^{\circ} -\frac{\angle BAC}{2},\\ \angle AMF &= 180^{\circ} -90^{\circ} -\frac{\angle ABC}{2}= 90^{\circ} -\frac{\angle ABC}{2}\\ \angle KMA &= 180^{\circ} -\angle AMB,\\ &= 180^{\circ} -\angle AIB,\\ &= 180^{\circ} -\big(180^{\circ}-\frac{\angle ABI}{2}-\frac{\angle BAI}{2}\big),\\ &= 90^{\circ}-\frac{\angle ACB}{2}. \end{align}$

From here, $\angle BMF+\angle AMF+\angle KMA=180^{\circ}.$

Acknowledgment

This problem and the solution have been posted by Emmanuel Antonio José García (Dominican Republic) at the CutTheKnotMath facebook page.

71548146