Problem 4 from the 2016 OBJM TST
Problem
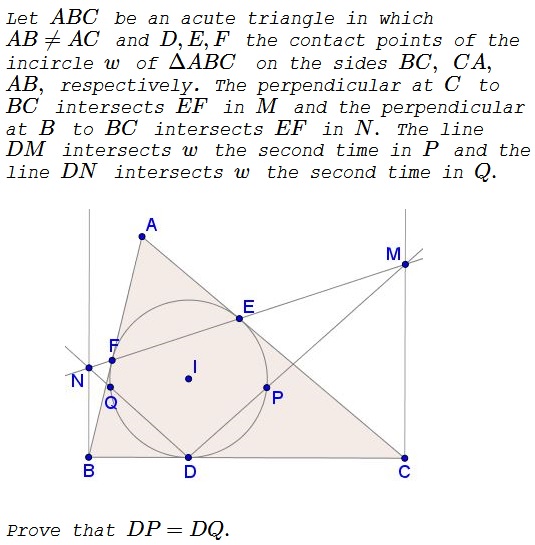
Solution
Let $S\,$ be the intersection of $EF\,$ and $BC.\,$
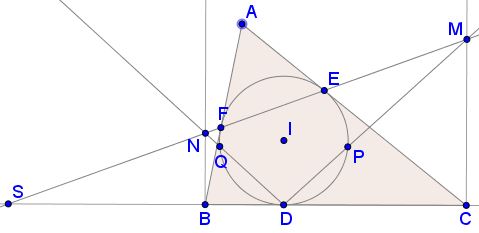
Menelaus' theorem in $\Delta ABC\,$ with the transversal $EFS\,$ gives
$\displaystyle \frac{SB}{SC}\cdot\frac{EC}{EA}\cdot\frac{FA}{FB}=1.$
Let, as usual, $a,b,c\,$ be the side lengths of $\Delta ABC,\,$ $p\,$ its semiperimeter. Then $EC=p-c,\,$ $EA=FA=p-a,\,$ and $FB=p-b,\,$ implying $\displaystyle \frac{SB}{SC}=\frac{p-b}{p-c}.$
Further, since $\Delta DBN\sim\Delta SCM,\,$ then also $\displaystyle \frac{BN}{CM}=\frac{p-b}{p-c}.\,$ Now, as before, $BD=p-b\,$ and $CD=p-c,\,$ so that $\displaystyle \frac{BN}{CM}=\frac{BD}{CD},\,$ and, since triangles $DBN\,$ and $DCM\,$ are right, they are also similar. Thus, in particular, $\angle BDN=\angle CDM,\,$ making the minor arcs $\overset{\frown}{DQ}=\overset{\frown}{DP}\,$ and, subsequently, $DP=DQ.$
Acknowledgment
The problem which is due to Ruben Dario and Leo Giugiuc has been kindly sent to me by Leo Giugiuc. The solution is the authors'.
Note that, as the solution shows, the statement is equally true in scalene triangles with no restriction on their angles:

![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73576004
