Problem 4 from the 4th BJMO Team Selection Test
Problem
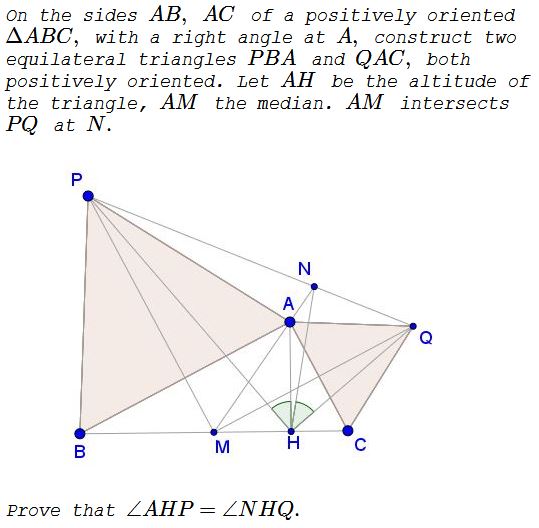
Solution 1
Our solution depends on a lemma that will be proved later on in two ways:
For the given configuration, the points $H,\,$ $M,\,$ $P,\,$ and $Q\,$ are concyclic:
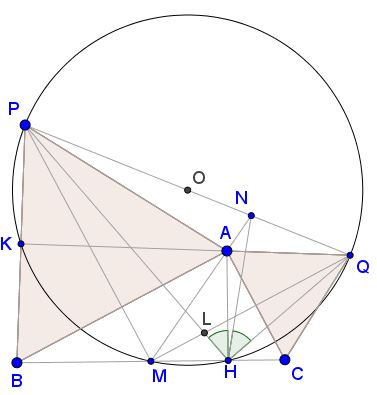
For $AB=AC\,$ the problem is trivial. WLOG. $AB\gt AC.\,$ Let $L\,$ be the intersection $PH\,$ and $MQ.\,$ From the cyclic quadrilateral $PMHQ,\,$ with $PM \perp MQ,\,$ we get also $PH\perp QH\,$ and $L\,$ is the orthocenter of the triangle made by $PQ,\,$ $PM\,$ and $QH.\,$ With $MH,\,$ one of the sides of its orthic triangle, and $ML,\,$ the bisector of $\angle AMC,\,$ we infer that $AM\,$ is another side of the orthic triangle, i.e. that $N\,$ is the foot of the altitude from the vertex made by $HQ\,$ and $PM,\,$ hence $L\,$ is the incenter of $\Delta MHN\,$ and, consequently, $HQ\,$ is the bisector of $\angle NHC,\,$ i.e. $\angle NHQ=\angle CHQ.$
But $\angle CHQ=180^{\circ}-\angle MHQ=\angle MPQ.\,$ And from the lemma, $\angle MPQ=90^{\circ}-\angle MQP=90^{\circ}-\angle MHP=\angle AHP,\,$ as required.
Proof 1 of Lemma
Let $K\,$ be the intersections of $AQ\,$ and $PB.\,$ $PB^2=AB^2=BH\cdot BC\,$ (1). Easy angle chasing shows that $AQ\perp PB,\,$ making $K\,$ the midpoint of $PB.\,$ Obviously, the quadrilaterals $APM\,$ and $AMCQ\,$ are kites, hence, $PM\perp MQ,\,$ making $PKMQ\,$ cyclic. Dividing by $2\,$ each side of (1) we get $BK\cdot BP=BM\cdot BH,\,$ putting $K\,$ on the circle $(PMQ)\,$ and, thus, proving the lemma.
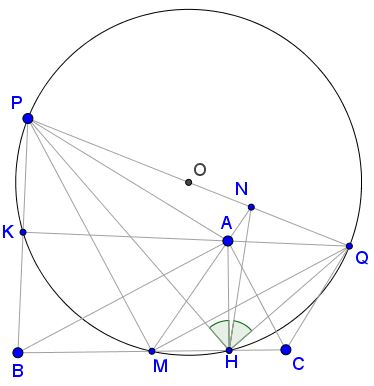
Proof 2 of Lemma
From $PB^2=AB^2=BH\cdot BC\,$ we infer that $PB\,$ is tangent to the circle $(PHC),\,$ so that $\angle HPB=\angle BCP,\,$ i.e., $\angle BPC=\angle PHB\,$ (3)
But in $\Delta PAQ,\,$ $\angle APQ+\angle AQP=30^{\circ}\,$ and, with $\angle APC=\angle APQ,\,$ we get
$\angle BPC=60^{\circ}-\angle APC=30^{\circ}+\angle AQP=\angle PQM.$
Applying (3) we complete the proof of the lemma.
Solution 2
We choose, WLOG, in the complex plane $A=2i,\,$ $\displaystyle B=-\frac{2}{k},\,$ and $C=2k,\,$ where $k\gt 0,\,$ so that $H=0\,$ and $\displaystyle M=k-\frac{1}{k}=\frac{k^2-1}{k}.$
$\Delta PBA\,$ is equilateral and positively oriented so that $P+Bu+Au^2=0,\,$ where $\displaystyle u=-\frac{1}{2}+\frac{\sqrt{3}}{2}i.\,$ From here $\displaystyle P=\frac{-(k\sqrt{3}+1)+(k+\sqrt{3})i}{k}.$
Similarly, from $\Delta QAC,\,$ $Q=(k+\sqrt{3})+(k\sqrt{3}+1)i.$
Let's find $\angle AHQ.\,$ We have
$\displaystyle \frac{A-H}{Q-H}=\frac{AH}{QH}(\cos\angle AHQ+i\sin\angle AHQ),\,$
implying
$\displaystyle \cot\angle AHQ=\frac{\displaystyle \mathbb{Re}\left(\frac{A-H}{Q-H}\right)}{\displaystyle \mathbb{Im}\left(\frac{A-H}{Q-H}\right)}=\frac{k\sqrt{3}+1}{k+\sqrt{3}}.$
Consider point $Z=a+bi,\,$ with $a,b\,$ real and $b\gt 0,\,$ such that $\Delta ZPH\,$ is positively oriented and $\angle ZHP=\angle AHQ.\,$ We have
$\displaystyle \frac{P-H}{Z-H}=\frac{PH}{ZH}(\cos\angle AHQ+i\sin\angle AHQ),$
from which $\displaystyle a=\frac{b(k^2-1)}{k^2\sqrt{3}+4k+\sqrt{3}}.\,$ From here we deduce the equation of the line $HZ:\,$ $(k^2\sqrt{3}+4k+\sqrt{3})x+(k^2-1)y=0.$
Also, the equations of the lines $AM\,$ and $PQ\,$ are
$\begin{cases} AM:& 2kx+(k^2-1)y=2(k^2-1)\;\text{and}\\ PQ:& -\sqrt{3}(k^2-1)x+(k^2+2k\sqrt{3}+1)y=4(k^2+k\sqrt{3}+1). \end{cases}$
Straightforward calculations show that
$\displaystyle \left|\begin{array}{ccc}\,k^2\sqrt{3}+4k+\sqrt{3}&k^2-1&0\\2k&k^2-1&2(k^2-1)\\-\sqrt{3}(k^2-1)&k^2+2k\sqrt{3}+1&4(k^2+k\sqrt{3}+1)\end{array}\right|=0,$
which says that the lines $HZ,\,$ $AM,\,$ and $PQ\,$ are concurrent. But $N\in HZ\,$ so that $\angle NHP=\angle ZHP\,$ and, since $\angle ZHP=\angle AHQ,\,$ $\angle NHP=\angle AHQ,\,$ as required.
Extension
On the sides $AB,\,$ $AC\,$ of the a positively oriented $\Delta ABC,\,$ with a right angle at $A\,$ construct two similar and positively oriented isosceles triangles $PBA\,$ and $QAC.\,$ Let $AH\,$ be the altitude of the triangle, $AM\,$ the median. $AM\,$ intersects $PQ\,$ at $N.$
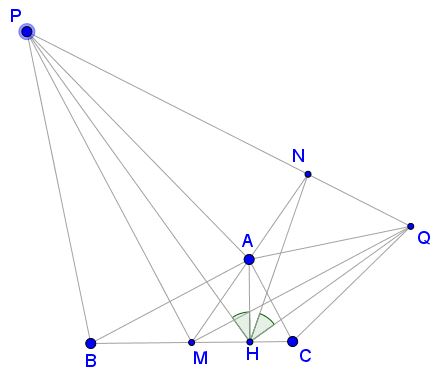
Prove that $\angle AHP = \angle NHQ.$
For a proof, note that we can specify, say, $\displaystyle v=-\frac{1}{2}+\frac{\mu}{2}i,\,$ with $\mu\gt 0,\,$ and set $P=(1-v)B+vA\,$ and $Q=(1-v)A+vC,\,$ so that in all the formulas in Solution 2, $\sqrt{3}\,$ will be replaced by $\mu,\,$ e.g., to start with, we find
$\displaystyle \begin{align} P&=\frac{-(k\mu+1)+(k+\mu)i}{k}\,\text{and}\\ Q&=(k+\mu)+(k\mu+1)i. \end{align}$
Thus, following Solution 2 we obtain the required result.
Note that the extension inherets many properties of the original problem. E.g., if $QA\perp PM\,$ and, if $K=QA\cap PM\,$ then $K,H\in (PQM),\,$ which follows by straaightforward angle chasing.
Acknowledgment
The problem is due to Miguel Ochoa Sanchez (Peru) and Leonard Giugiuc (Romania), Solution 1 (with the lemma and its to proofs) to Stan Fulger (Romania). Solution 2 is by Leo Giugiuc. Solution 2 admits a modification that allows to extend the problem.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579291
