Circumcenter and Orthocenter
What Might This Be About?
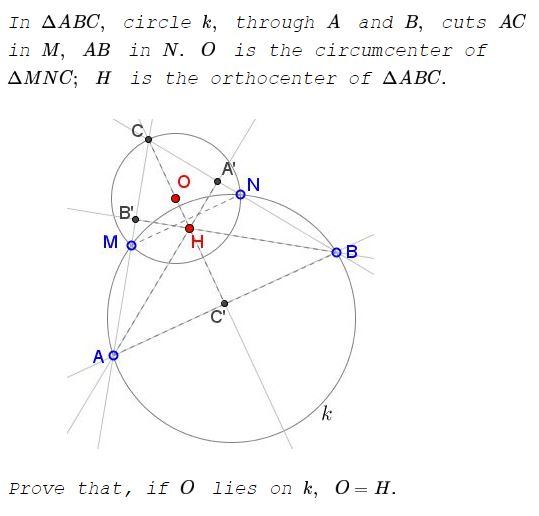
Problem
Proof 1
The problem is solved by angle chasing.
First note that $MN\;$ is an antiparallel in $\Delta ABC,\;$ meaning that $\angle MNC=\angle BAC\;$ and $\angle NMC=\angle ABC.$
Next, observe that $AO\;$ always passes through $H\;$ and thus is an altitude $CC'$ in $\Delta ABC.\;$ Indeed, triangles $MON,\;$ $NOC,\;$ and $COM\;$ are isosceles, say, $\nu=\angle MCO=\angle CMO;\;$ $\mu=\angle CNO=\angle NCO;\;$ $\gamma=\angle NMO=\angle MNO.$
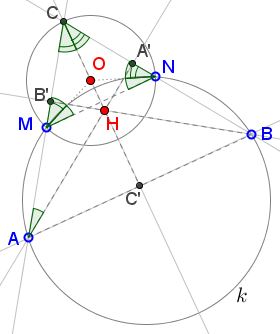
$\angle BAC=\angle MNC=\gamma+\mu.\;$ On the other hand, $\mu+\nu+\gamma=90^{\circ},\;$ so that $\nu=90{\circ}-\mu=\gamma,\;$ implying that $\Delta ACC',\;$ where $C'\;$ is the point of intersection of $CH\;$ with $AB,\;$ is right, with $\angle AC'C=90^{\circ},\;$ making $CC'\;$ an altitude in $\Delta ABC\;$ and $H\in CC'.$
If $AA'$ is another altitude in $\Delta ABC,\;$ then
$\angle HAM=\angle A'AC=90^{\circ}-\nu-\mu=\gamma=\angle ONM.\;$
Having $O\in k,\;$ means, in part, that $\angle ONM\;$ is inscribed in $k\;$ and being subtended by the arc $MO.\;$ If $AA'$ crosses $k\;$ in say $O'\;$ then $\angle A'AM\;$ which is equal to $\angle ONM\;$ will be subtended by the arc $MO',\;$ implying that $O'=O\;$ and, hence, that $AA'$ is passing through $O.\;$ Thus $O\;$ lies at the intersection of two altitudes $CC'\;$ and $AA'\;$ of $\Delta ABC,\;$ causing $H=O.$
Proof 2
Let $k\;$ be a circle through $A\;$ and $B\;$ and denote by $M\;$ and $N\;$ the second intersections of $k\;$ with the sidelines $CA\;$ and $CB,\;$ respectively $(N\;$ has nothing to do with the nine-point center!). Then $MN\parallel B'A'.\;$ There is thus a homothety with center at $C\;$ (of ratio $t,\;$ say) that maps the circumcircle of $CB'A'\;$ (centered at the midpoint of $CH)\;$ to the circumcircle of $CMN.\;$ The same homothety maps the nine-point circle of $ABC\;$ to a circle $k'\;$ through $M, N,\;$ and the circumcenter $O\;$ of $CMN.\;$ It follows that $O\;$ lies on $k\;$ if and only if $A\;$ lies on $k',\;$ that is, if and only if $t=2.$
Acknowledgment
The problem has been posted at the CutTheKnotMath facebook page on June 5, 2016 by Emil Stoyanov (Bulgaria). Proof 2 is by Grégoire Nicollier.
|Contact| |Front page| |Contents| |Geometry| |Generalizations|
Copyright © 1996-2018 Alexander Bogomolny73570412
