Stan Fulger's Observation in Right Triangle
What Is This About?
Source

Problem
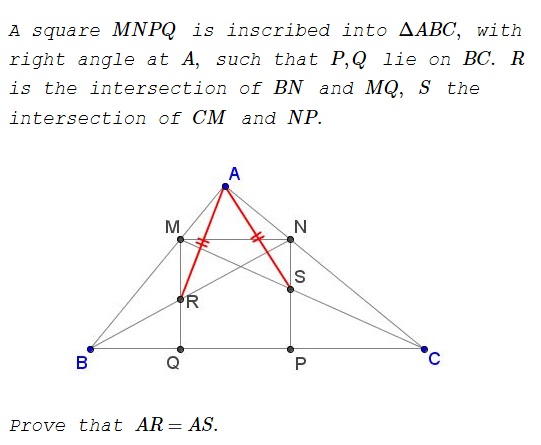
Solution
First off, let's find the side of the square in terms of the side lengths $a,b,c\,$ of the triangle.
If $x=MN=MQ,\,$ $h\,$ the altitude in $\Delta ABC\,$ from $A,\,$ then using the similarity of triangles $ABC\,$ and $AMN,\,$ $\displaystyle\frac{h-x}{h}=\frac{x}{a},\,$ wherefrom $x=\displaystyle\frac{ha}{h+a}.\,$
Recollecting that the area of a right triangle can be computed in two ways, we get $bc=ha,\,$ of $\displaystyle h=\frac{bc}{a}.\,$ Combining the two expressions gives
$\displaystyle x=\frac{abc}{a^2+bc}.$
It follows that $\displaystyle AM=\frac{bc^2}{bc+a^2}\,$ and $\displaystyle AM=\frac{b^2c}{bc+a^2}.\,$ Now then, from the similarity of triangles $AMN\,$ and $QBM,\,$ $BQ=\displaystyle\frac{ac^2)(bc+a^2}\,$ and, similarly, $\displaystyle CP=\frac{ab^2}{bc+a^2}.$
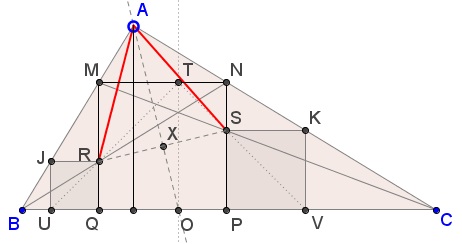
From the construction, there's a square, $JUQR\,$ with $J\,$ on $AB\,$ and $U\,$ on $BC.\,$ We can again use similarity of triangles or remark that $QJ\,$ is an angle bisector in $\Delta BQM\,$ and find its length with a well-known formula. Thus, we can find the side of the square $\displaystyle QR=\frac{ab^2c}{(bc+a^2)(b+c)}.\,$ Similarly, $\displaystyle PS=\frac{abc^2}{(bc+a^2)(b+c)}.\,$ Note that $QR+PS=x,\,$ implying $PS=MR\,$ and $QR=NS\,$ such that $RS\,$ go0es through the center $X\,$ of the square $MNPQ.\,$ In particular, $RX=SX.$
If now $O\,$ is the midpoint of $UV,\,$ then,
- $OP:OQ=b:c=QR:PS\,$ and
- $BO:CO=(BQ+PS):(CP+QR)=c:b.$
It follows that $AO\,$ bisects angle $BAC\,$ and, denoting its intersection with $MN\,$ as $O',\,$ $MO':NO'=c:b\,$ so that $OO'\,$ passes through $X\,$ and is perpendicular to $RS.\,$ In $\Delta RAS,\,$ $AX\,$ serves as the median and the altitude from $A\,$ which makes the triangle $isosceles:\,$ $AR=AS.$
Acknowledgment
This problem by Stan Fulger has been posted at the Peru Geometrico facebook group by Miguel Ochoa Sanchez.
Source

Problem

Solution
First off, let's find the side of the square in terms of the side lengths $a,b,c\,$ of the triangle.
If $x=MN=MQ,\,$ $h\,$ the altitude in $\Delta ABC\,$ from $A,\,$ then using the similarity of triangles $ABC\,$ and $AMN,\,$ $\displaystyle\frac{h-x}{h}=\frac{x}{a},\,$ wherefrom $x=\displaystyle\frac{ha}{h+a}.\,$

Recollecting that the area of a right triangle can be computed in two ways, we get $bc=ha,\,$ of $\displaystyle h=\frac{bc}{a}.\,$ Combining the two expressions gives
$\displaystyle x=\frac{abc}{a^2+bc}.$
It follows that $\displaystyle AM=\frac{bc^2}{bc+a^2}\,$ and $\displaystyle AM=\frac{b^2c}{bc+a^2}.\,$ Now then, from the similarity of triangles $AMN\,$ and $QBM,\,$ $BQ=\displaystyle\frac{ac^2)(bc+a^2}\,$ and, similarly, $\displaystyle CP=\frac{ab^2}{bc+a^2}.$
From the construction, there's a square, $JUQR\,$ with $J\,$ on $AB\,$ and $U\,$ on $BC.\,$ We can again use similarity of triangles or remark that $QJ\,$ is an angle bisector in $\Delta BQM\,$ and find its length with a well-known formula. Thus, we can find the side of the square $\displaystyle QR=\frac{ab^2c}{(bc+a^2)(b+c)}.\,$ Similarly, $\displaystyle PS=\frac{abc^2}{(bc+a^2)(b+c)}.\,$ Note that $QR+PS=x,\,$ implying $PS=MR\,$ and $QR=NS\,$ such that $RS\,$ go0es through the center $X\,$ of the square $MNPQ.\,$ In particular, $RX=SX.$
If now $O\,$ is the midpoint of $UV,\,$ then,
- $OP:OQ=b:c=QR:PS\,$ and
- $BO:CO=(BQ+PS):(CP+QR)=c:b.$
It follows that $AO\,$ bisects angle $BAC\,$ and, denoting its intersection with $MN\,$ as $O',\,$ $MO':NO'=c:b\,$ so that $OO'\,$ passes through $X\,$ and is perpendicular to $RS.\,$ In $\Delta RAS,\,$ $AX\,$ serves as the median and the altitude from $A\,$ which makes the triangle $isosceles:\,$ $AR=AS.$
Acknowledgment
This problem by Stan Fulger has been posted at the Peru Geometrico facebook group by Miguel Ochoa Sanchez.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73568956
