Equilateral Triangle in Square And the Pedal Circle of Its Apex
Problem

Solution
Choose $D=(-1,1),\,$ $B=(1,1).\,$ Then $P=(0,\displaystyle \sqrt{3}-1),\,$ $X=(0,1),\,$ $Z=(1,\sqrt{3}-1),\,$ and $Y=\displaystyle \left(-\frac{\sqrt{3}-1}{2},\frac{\sqrt{3}-1}{2}\right).\,$ Let $F\,$ be the center of the circle $(XYZ),\,$ then it can be verified that $F=\displaystyle \left(\frac{\sqrt{3}-1}{2},\frac{\sqrt{3}-1}{2}\right).\,$ (For a verification simply check that $FX=FY=FZ=\sqrt{3}-1.)$
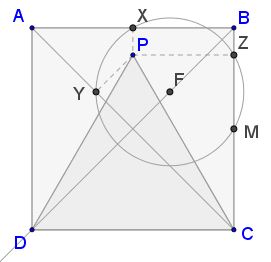
In particular $F\in BD\,$ so that the circle is symmetric in $BD\,$ and so are its intersections with $AB\,$ and $BC.\,$ It follows that, since $X\,$ is the midpoint of $AB,\,$ $M\,$ is the midpoint of $BC.$
Extra
Equilateral triangle $CDP\,$ is erected in the interior of square $ABCD.\,$ $X',Y,Z'\,$ are the pedal points of $P\,$ in $\Delta ACD.\,$ Circle $(X'YZ')\,$ intersects $AD\,$ the second time in $E.\,$
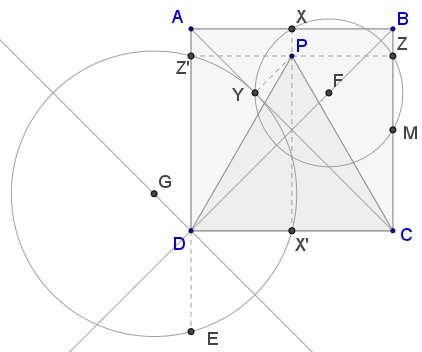
Prove $2\cdot DE=AD.$
Acknowledgment
Tran Quang Hung has kindly posted that problem of his at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574013
