Equilateral Triangle in Square and Its Circumcircle
Source
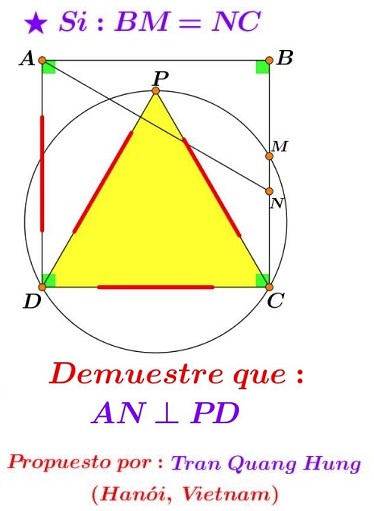
Problem
Solution 1
Choose $P=(1,0),\,$ $\displaystyle D=\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right),\,$ $\displaystyle C=\left(-\frac{1}{2},-\frac{\sqrt{3}}{2}\right),\,$ such that $\displaystyle B=\left(\frac{2\sqrt{3}-1}{2},-\frac{\sqrt{3}}{2}\right),\,$ $\displaystyle A=\left(\frac{2\sqrt{3}-1}{2},\frac{\sqrt{3}}{2}\right),\,$ $\displaystyle M=\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right),\,$ from which $\displaystyle N=\left(\frac{2\sqrt{3}-3}{2},-\frac{\sqrt{3}}{2}\right).$
It follows that the slope of $AN\,$ is $\sqrt{3},\,$ while the slope of $PD\,$ is clearly $\displaystyle -\frac{1}{\sqrt{3}}.$
Solution 2
Let $CN=BM=x\,$ and $MN=y.$
$\angle MCP=30^{\circ},\,$ $\angle PMC=120^{\circ},\,$ hence, $\angle CPM=30^{\circ}\,$ and, subsequently, $PM=x+y.\,$
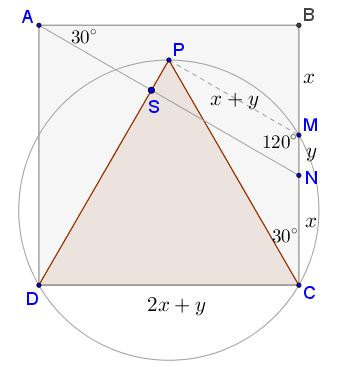
$PC=(x+y)\sqrt{3}=2x+y,\,$ so that $x=y(\sqrt{3}+1).\,$ It follows that $BN=x+y=y(\sqrt{3}+2),\,$ whereas $AB=CD=2x+y=y(2\sqrt{3}+3).\,$ Thus $\tan\angle NAB=\displaystyle \frac{\sqrt{3}+2}{2\sqrt{3}+3}=\frac{1}{\sqrt{3}}.\,$ We conclude that $\angle NAB=30^{\circ}\,$ such that, indeed, $AN\perp DP.$
Solution 3
With a reference to the diagram below, $PM=PK.$
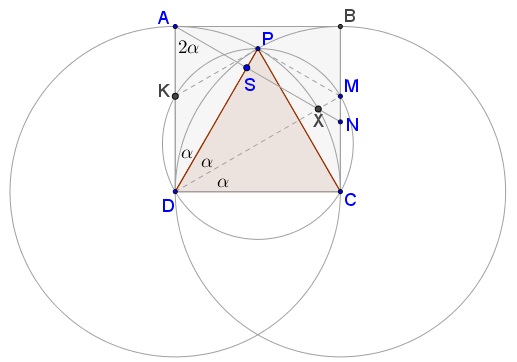
$\Delta PMD=\Delta CMD,\,$ implying $MP=MC,\,$ so that $\angle MPD=90^{\circ}.$
Further, $\angle ADP=\angle PDM=\angle MDC=\alpha.\,$ From $XA=XD,\,$ $\angle XAD=2\alpha,\,$ making $\angle ASD=90^{\circ},$ because $\angle SAD+\angle SDA=3\alpha=90^{\circ}.$
Solution 4
With a reference to the diagram below, $\angle CMD=\angle CPD=60^{\circ}\,$ and $\angle PMD=\angle PCD=60^{\circ},\,$ so that $\angle PMD=\angle CMD=60^{\circ}.\,$

By symmetry, $\angle GNM=\angle GMN=\angle CMD=60^{\circ}.\,$ Thus, $\angle NGM=\angle AGD=60^{\circ}.\,$ $\Delta ADG\,$ is equilateral and has a base at $90^{\circ}\,$ to the base of $\Delta DCP.\,$ Their corresponding sides are also perpendicular: $AG\perp DP\,$ and $DG\perp CP.$
Solution 5
$AM'=BM=CN\,$ and $AM'\parallel CN\,$ meaning that $AN\parallel CM'.$
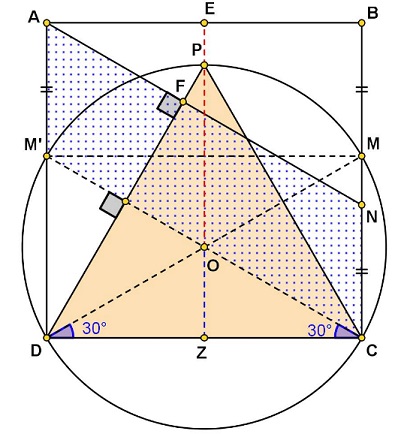
$CM=DM'\,$ and $CM\parallel DM'\,$ so that $CMM'D\,$ is a rectangle because $DM'\perp CD.\,$ Thus $CM'\,$ and $DM\,$ are diameters of circle $(CDP),\,$ with the center at $O.\,$ Thus, $\angle COD=120^{\circ}\,$ and $\angle M'CD=30^{\circ},\,$ making $CM'\perp DP\,$ and, subsequently, $AN\perp DP.$
Solution 6
With a reference to the diagram below and by pure angle chasing, from SAS, $\Delta ABN=\Delta DCM.\,$ Also $\angle DMC=\angle DPC=60^{\circ},\,$ s $\angle MDC=30^{\circ},\,$ $\angle MDP=30^{\circ},\,$ $\angle FDA=30^{\circ}.$

Also $\angle BAN=\angle MDC=30^{\circ},\,$ so $\angle FAD=60^{\circ}.\,$ Hence, $\angle FAD+\angle FDA=90^{\circ}\,$ and $\angle AFD=90^{\circ}.$
Solution 7
Since $BM=NC,\,$ $AMND\,$ is an isosceles trapezoid, thus $AN=DM\,$ and also $AE=DE,\,$ implying that $\Delta ADE\,$ is isosceles.

$\angle D_2=\angle C_1=30^{\circ}\,$ and $\angle D_1=\angle C_1=30^{\circ}\,$ (since $DMPC\,$ is cyclic), thus $\angle ADE=60^{\circ}.$
It follows that $\Delta ADE\,$ is equilateral, $DF\,$ is its angle bisector so that it is also an altitude, meaning $AN\perp DF.$
Acknowledgment
I am grateful to Leo Giugiuc who supplied a solution (Solution 1) and a link to the original post at the Peru Geometrico facebook group of the problem by Tran Quang Hung. Solution 2 is by Bariş Altay; Solution 3 is by Nguyen Ngoc Tú Solution 5 is by Ενθύμης Αλεξιον; Solution 6 is by Julius Geyser; Solution 7 is by Stelios Karpathios (translated by Takis Chronopoulos).
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579800
