A Triangle in a Rhombus with a 60 Degrees Angle
What Is This About?
Problem
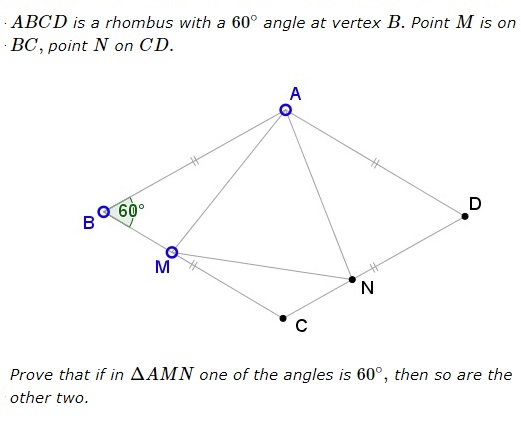
Solution 1
First assume that the angle at $A$ is $60^{\circ}.$ Then note that, if one of the points - $M$ or $N$ - moves, then all of the angles of $\Delta AMN$ change. For example, if $M$ moves to a position $M',$ still on $BC:$
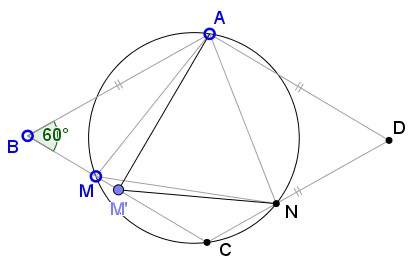
Then clearly the angles at $A$ and $N$ change. This is also true for the angle at $M$ because the circumcircle $(AMN)$ passes through $C$ such that, on the chord $MC$ all angles $AM'N$ are different from $\angle AMN.$
If $R_{A}$ is the counterclockwise rotation around $A$ through $60^{\circ},$ then $R_{A}(B)=C$ and $R_{A}(C)=D,$ so that $R_{A}(M)\in CD.$ If $R_{A}(M)=N'\ne N,$ then $\angle MAN'=60^{\circ},$ and, from the above, $\angle MAN\ne\angle MAN',$ contradicting the assumption that $\angle MAN=60^{\circ}.$ As a consequence, $AM=AN$ so that $\Delta AMN$ is isosceles and, therefore, also equilateral.
Assume now that, say, $\angle AMN=60^{\circ}$ and let $R_{M}$ denote the clockwise rotation around $M$ through $60^{\circ}.$ Then $R_{M}(B)=B'\in AB,$ $R_{M}(AB)=B'N'\parallel BC$ and $B'N'=BA.$ It follows that $N'\in CD$ and, if $N'\ne N,$ $\angle AMN\ne\angle AMN'=60^{\circ}.$ A contradiction. Thus $N'=N$ and $NA=MN,$ making $\Delta AMN$ isosceles and, consequently, equilateral.
The case where $\angle ANM=60^{\circ}$ is similar to the above.
Solution 2
If $\angle MAN=60^{\circ},$ triangles $ABM$ and $ACN$ are congruent (ASA), so $AM=AN,$ implying $\Delta AMN$ is isosceles and, hence, equilateral.
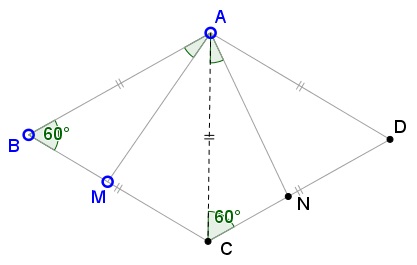
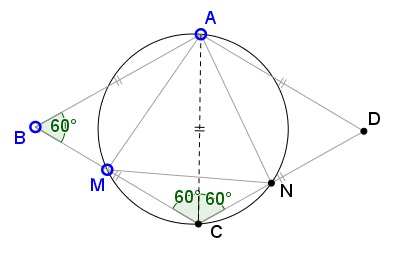
If $\angle AMN=60^{\circ},$ $\angle AMN=\angle ACN,$ so that $A,M,N,C$ are concyclc. It follows that $\angle ANM=\angle ACM=60^{\circ}.$
Acknowledgment
This is a problem by V. Proizvolov that was published in the Russian Kvant magazine (n 2, 1991, p 34). Solution 2 is by Vincent Pantaloni.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581122
