The Shortest Distance in a Circular Segment
What Might This Be About?
Problem
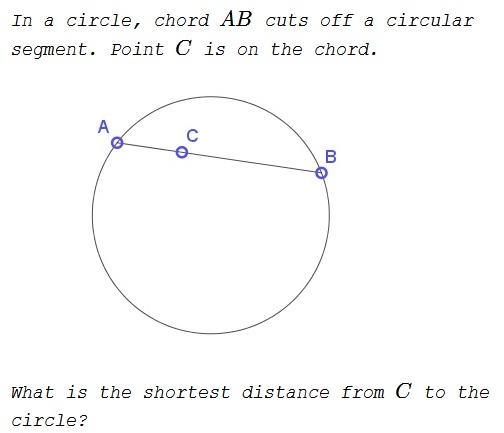
Solution
A proof without words for finding the point $X$ to connect to:

Point $X$ that lies on the diameter through $C$ is the answer. To see that, suffice it to consider circle $C(C,X)$ through $X$ with the center at $C.$ That circle is tangent to the given one, because the tangents at $X$ to both circles are perpendicular to $OX$ (and $CX.)$
From the Intersecting Chords theorem, $AC\cdot BC=CX\cdot (2R-CX),$ where $R$ is the radius of the given circle. It follows that $CX$ is the shortest of $R\pm\sqrt{R^2-AC\cdot BC).$
Acknowledgment
![]()
|Contact| |Front page| |Contents| |Geometry| |Triangle constructions|
Copyright © 1996-2018 Alexander Bogomolny73575238
