Igor Sharygin's Problem in Circumscribed Quadrilateral
Source
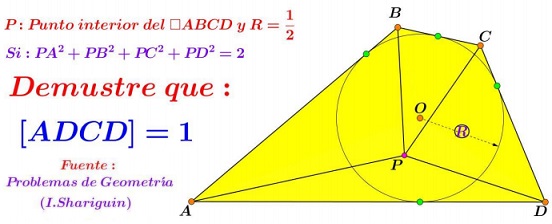
Problem

Solution
We have
$AP^2+BP^2\ge 2\cdot AP\cdot BP\ge 4[ABP]\\ BP^2+CP^2\ge 2\cdot BP\cdot CP\ge 4[BCP]\\ CP^2+DP^2\ge 2\cdot CP\cdot DP\ge 4[CDP]\\ DP^2+AP^2\ge 2\cdot DP\cdot AP\ge 4[DAP].$
Summing up we obtain
$2(AP^2+BP^2+CP^2+DP^2)\ge 4[ABCD],$
with the conclusion $[ABCD]\le 1.\,$ But $[ABCD]=sR=\displaystyle\frac{s}{2},\,$ implying $s\le 2,\,$ where $s\,$ is the semiperimeter of $ABCD.\,$ Now, according to a result of Ivanova(1975), $s\ge 4R,\,$ with equality only when $ABCD\,$ is a square. From $2\ge s\ge 4R=2,\,$ it follows that $s=4R,\,$ so that $ABCD$ is a square, with half the side length $R=\displaystyle\frac{1}{2},\,$ making $[ABCD]=1.$
Acknowledgment
The problem by the late Russian geometer Igor Sharygin has been posted at the PERU GEOMETRICO facebook group and commincated to me by Leo Giugiuc, along with a solution of his.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518526
