Segment Trisection II
What Is That about?
Problem
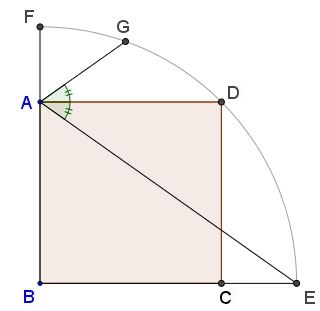
Solution
Complete the circle and let $FF',\,$ and $EE'\,$ be its diameters, and $G'\,$ the reflection of $G\,$ in $BF.\,$
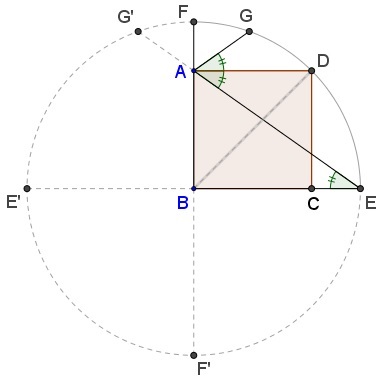
Assuming the radius of the circle equals $1,\,$ the side of the square $\displaystyle AB=\frac{1}{\sqrt{2}}.\,$ Then $AE^2=BE^2+AB^2,\,$ wherefrom $AE=\displaystyle \sqrt{\frac{3}{2}}.\,$
Since $\angle EAD=\angle DAG,\,$ $G',\,$ $A,\,$ and $E\,$ are collinear. By the Intersecting Chords theorem,
$\displaystyle AG=AG'=\frac{AF\cdot AF'}{AE}= \frac{\displaystyle \left(1-\frac{1}{\sqrt{2}}\right)\left(1+\frac{1}{\sqrt{2}}\right)}{\displaystyle\sqrt{\frac{3}{2}}} =\sqrt{\frac{1}{6}}.$
Thus $\displaystyle \frac{AE}{AG}=\frac{\displaystyle \sqrt{\frac{3}{2}}}{\displaystyle \sqrt{\frac{1}{6}}}=3.$
Acknowledgment
The problem has been posted on twitter with a GeoGebra illustration by Tim Brzezinski. This page is an attempt to learn Tim's technique and the process of creating animated gif files. Tim has credited _eylem_99. I understand there was a chain of retweets.
This is a second example of a serendipitous segment trisection. The first one dealt with two medians in a triangle.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572164
