Circle Concurrence on Circumcircle
What Might This Be About?
Problem
$P$ is a point in the plane of $\Delta ABC.$ $P_a,P_b,P_c$ are the reflections of $P$ in the perpendicular bisectors of sides $BC,$ $AC,$ and $BC,$ respectively.
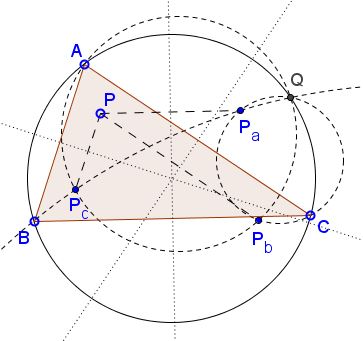
Then, the circles $(AP_bP_c),$ $(BP_aP_c),$ $(CP_aP_b)$ are concurrent at the circumcircle of $(ABC).$
Proof
Let Q be the second intersection of $(AP_bP_c)$ with the circumcircle $(ABC)=(O)$. Since $O$ is on perpendicular bisector of $AQ$ and $OP=OP_b=OP_c,$ by obvious symmetry it follows that the cyclic $AQP_bP_c$ is an isosceles trapezoid with $AQ \parallel P_bP_c.$ Now let $\ell_a$ be the parallel to $P_bP_c$ through $P$ and let $\tau_a$ be the tangent of $(PP_bP_c)$ at $P.$
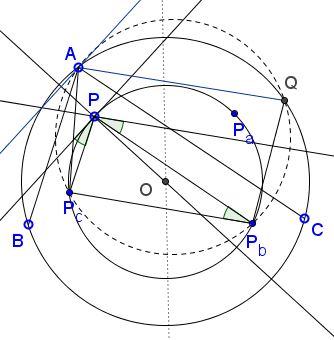
Then $\angle (PP_b,\ell_a)=\angle (P_bP,P_bP_c)=\angle(\tau_a,PP_c).$ Therefore, $\ell_a$ and $\tau_a$ are isogonals wrt $\angle P_bPP_c.$ But since $\ell_a \parallel P_bP_c \parallel AQ,$ $PP_b \parallel AC$ and $PP_c \parallel AB,$ it follows that $AQ$ is the isogonal of the perpendicular from $A$ to $OP$ wrt $\angle BAC$ (because that perpendicular is parallel to $\tau_a).$ Now, the isogonal conjugates of the lines perpendicular to $OP$ through $B$ (wrt to $\angle ABC)$ and through $C$ (wrt to $\angle ACB)$ both pass through $Q.$ Which means that $Q$ is the isogonal conjugate of the infinite point of a perpendicular to $OP$ wrt $\triangle ABC.$
Similarly, circles $(BP_cP_a)$ and $(CP_aP_b)$ hit $(O)$ again at $Q.$
Acknowledgment
The theorem on this page has been discovered by Emmanuel Antonio José García (Dominican Republic). The proof is due to Luís González.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579325
