Inverse Similarity through Reflections
What Might This Be About?
Problem
Let $P$ and $Q$ be two points in $\Delta ABC;$ lines $\ell_a,$ $\ell_b,$ $\ell_c$ through $Q$ be perpendicular to the sides $BC,$ $AC,$ and $AB,$ respectively; $P_a,$ $P_b,$ $P_c$ be reflections of $P$ in $\ell_a,$ $\ell_b,$ $\ell_c.$
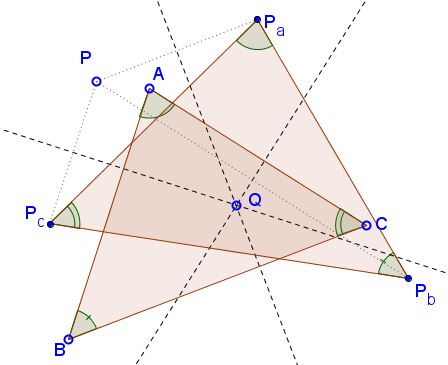
Then $\Delta P_aP_bP_c$ is inversely similar to $\Delta ABC.$
Proof
The proof is by angle chasing for which the following diagram may serve as a road map.
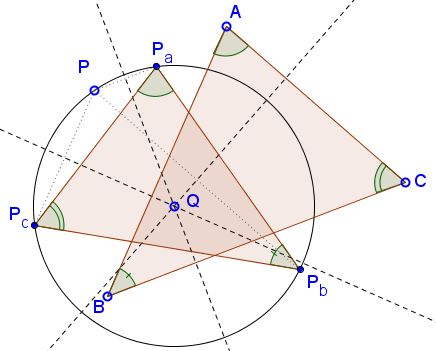
Extension
Define $Q_a,$ $Q_b,$ $Q_c$ as the reflections of $Q$ in $P_a,$ $P_b,$ $P_c.$ Then obviously $\Delta Q_aQ_bQ_c$ is a homothetic image of $\Delta P_aP_bP_c$ and is, therefore similar to the latter. The same is true for $\Delta M_aM_bM_c,$ where points $M$ are midway between the corresponding points $P$ and $Q.$
In particular this is true when $Q=H,$ the orthocenter of $\Delta ABC,$ and $P=O,$ the circumcenter of the latter.
Acknowledgment
The above is a reflection on private communication from Leo Giugiuc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575522
