Reflection in the Circumcenter

What Might This Be About?

Problem

Points $A_1,$ $B_1,$ $C_1$ are projections of point $P$ on the sides $BC,$ $AC,$ $AB$ of $\Delta ABC .$ Points $A_2,$ $B_2,$ $C_2$ are the respective reflections of $A_1,$ $B_1,$ $C_1$ in the midpoints $M_a,$ $M_b,$ and $M_c$ of those sides.

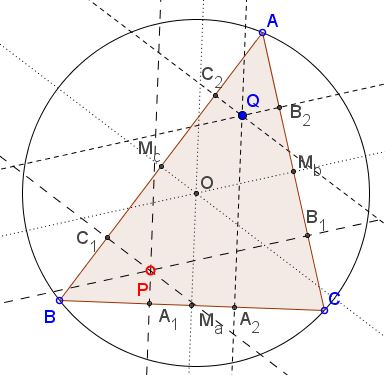
reflection in circumcenter - problem

Prove that the perpendiculars at $A_2,$ $B_2,$ $C_2$ to the sides $BC,$ $AC,$ $AB,$ respectively, are concurrent.

Solution 1

Let $O$ be the circumcenter of $\Delta ABC.$ The projections (or pedal) points of $O$ are exactly the midpoints of the sides.

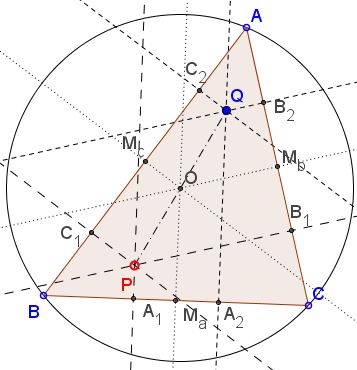
reflection in circumcenter - problem

Define $Q$ to be the reflection of $P$ in $O.$ By Thales' Intercepts Theorem, the projections of $P$ and $Q$ on the sides are equidistant from the midpoints of the sides; $A_2,$ $B_2,$ $C_2$ are, therefore, the projections of $Q,$ and this proves the statement.

Solution 2

The statement is a direct consequence of Carnot's theorem, according to which $AC_{1}^{2} - BC_{1}^{2} + BA_{1}^{2} - CA_{1}^{2} + CB_{1}^{2} - AB_{1}^{2} = 0.$ But, because $AC_{1}=BC_{2},$ $AC_{2}=BC_{1},$ etc., this is equivalent to

$AC_{2}^{2} - BC_{2}^{2} + BA_{2}^{2} - CA_{2}^{2} + CB_{2}^{2} - AB_{2}^{2} = 0,$

which implies the concurrency of the perpendiculars at the second set of the points.

Acknowledgment

The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. He also supplied the second solution.

72104692