Quadrilateral Inscribed into Parallelogram
Problem
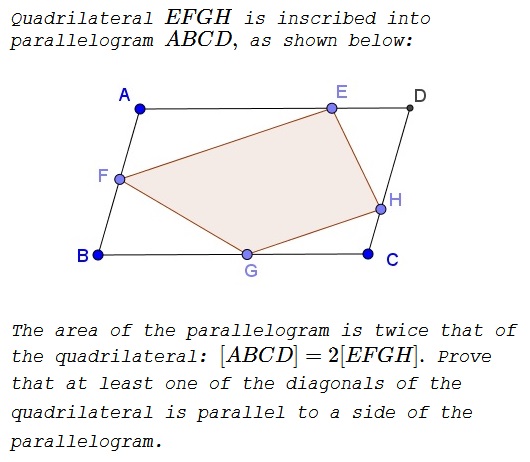
Solution 1
The problem is simple enough to be solved with a couple of references to Euclid's Elements. According to Euclid I.38:
Triangles which are on equal bases and in the same parallels equal one another.
Euclid I.39 is the converse:
Equal triangles which are on the same base and on the same side are also in the same parallels.
Consider point $P$ on $AD$ such that $PG\parallel AB.$
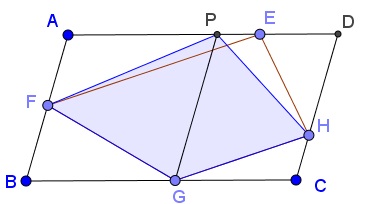
If $P=E,$ there is nothing to prove. Otherwise, due to Euclid I.38, $[PFGH]=[\Delta AGD]=\displaystyle \frac{1}{2}[ABCD]=[EFGH].$ From Euclid's first notions then, $[\Delta PFH]=[\Delta EFH],$ which, by Euclid I.39, is only possible if $FH\parallel AD.$
Solution 2
Let, $\vec{BC}=\vec{u}$ and $\vec{BA}=\vec{v}$. Thus, for some scalars $p$ and $q$,
$\displaystyle \begin{align} \vec{GE}&=\vec{CD}+(\vec{GC}-\vec{ED})=\vec{v}+p\vec{u}, \\ \vec{FH}&=\vec{BC}+(\vec{CH}-\vec{BF})=\vec{u}+q\vec{v}. \\ \\ A(ABCD)&=|\vec{BC}\times\vec{BA}|=|\vec{u}\times\vec{v}|, \\ 2\cdot A(EFGH)&=|\vec{GE}\times\vec{FH}|=|(\vec{v}+p\vec{u})\times(\vec{u}+q\vec{v})| \\ &=|(pq-1)\vec{u}\times\vec{v}|=|pq-1||\vec{u}\times\vec{v}|. \end{align}$
$A(ABCD)=2\cdot A(EFGH)~\Rightarrow$ $pq=2$ or $pq=0$. If $pq=2$, then $|p|\geq \sqrt{2}$ or $|q|\geq \sqrt{2}$. WLOG, let $|p|\geq \sqrt{2}$. This is not possible because $\vec{GE}=\vec{v}+p\vec{u}$ implies that to get to point $E$ from $G$, we traverse parallel to $BA$ upto the line $AD$, and then move along the line in one of the two possible directions by a distance equal to $|p|$ times $|AD|$. If $|p|\geq \sqrt{2}$, then this would put the point $E$ outside the line segment $AD$ on line $AD$. Thus $pq=0$ and either (or both) $p$ and $q$ are zero. Thus, $\vec{GE}=\vec{v}=\vec{BA}$ or/and $\vec{FH}=\vec{u}=\vec{BC}$.
Solution 3

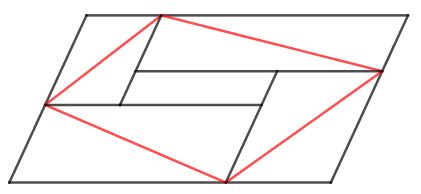
Acknowledgment
This is problem M13 from the Quantum magazine (Sept/Oct 1990). The problem is attributed to V. N. Dubrovsky.
Solution 2 is by Amit Itagi; Solution 3 is by Grégoire Nicollier.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578395
