Proportions with Two Orthocenters
What is this about?
Source
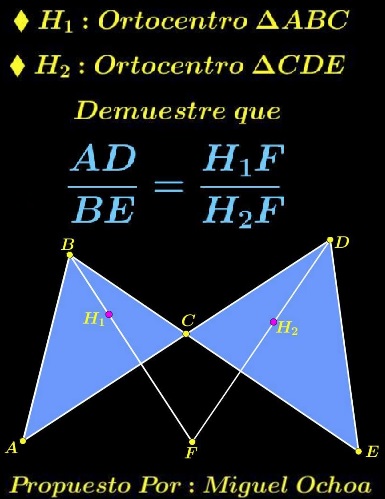
Problem
Lines $AD\;$ and $BE\;$ intersect in $C,\;$ thus forming two triangles, $ABC\;$ and $CDE.\;$ Let $H_1,H_2$ be the orthocenters of the two triangles, and let $BH_1\;$ and $DH_2\;$ meet in $F.$
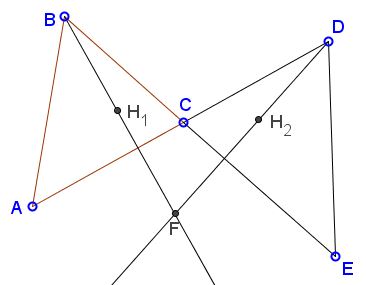
Then
$\displaystyle\frac{AD}{BE}=\frac{FH_1}{FH_2}.$
Solution 1
We choose $A=(-a,0),\;$ $B=(0,1),\;$ and $C=(c,0),\;$ where $a,c\gt 0\;$ and $ac\lt 1.\;$ Then $H_1=(0,ac).$
Let $F=(0,-k),\;$ with $k\gt c^2.\;$ Thus, $FD\;$ is defined by $cx-y=k\;$ and from here $\displaystyle D=\left(\frac{k}{c},0\right).$
Let $M=(m,0)\;$ be the projection of $H_2\;$ on $CD,\;$ where $m\;$ is chosen such that $\Delta CDE\;$ is acute angled. Making the intersections of the vertical line $x=c\;$ with the lines $FD\;$ and $AC\;$ we get $\displaystyle E=\left(m,1-\frac{m}{k}\right)\;$ and $H_2=(m,mc-k),\;$ respectively. From all this, we obtain $\displaystyle AD=\frac{ac+k}{c},\;$ $\displaystyle BE=\frac{\sqrt{c^2+1}}{c},\;$ $FH_1=ac+k,\;$ and $FH_2=m\sqrt{c^2+1}\;$ which proves that $\displaystyle\frac{AD}{BE}=\frac{FH_1}{FH_2}.$
Solution 2
Draw the altitudes from $A\;$ in $\Delta ABC\;$and from $E\;$ in $\Delta CDE.\;$ Let $G_1\;$ be the intersection of $BF\;$ and $AD,\;$ $G_2\;$ the intersection of $DF\;$ and $BE.$
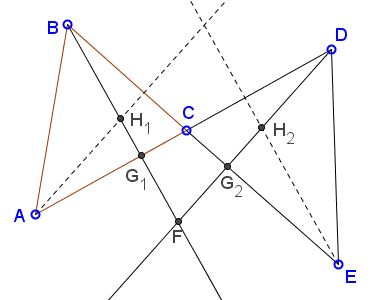
There are several similar triangles: $AG_1H_1,\;$ $DFG_1,\;$ $EG_2H_2,\;$ $BFG_2\;$ which gives us a sequence of proportions:
$\displaystyle\frac{AG_1}{DG_1}=\frac{G_1H_1}{FG_1},$
implying $\displaystyle\frac{AD}{FH_1}=\frac{DG_1}{FG_1}.$ But
$\displaystyle\frac{DG_1}{FG_1}=\frac{EG_2}{G_2H_2}=\frac{BG_2}{FG_2}=\frac{BE}{FH_2}.$
Acknowledgment
The problem due to Miguel Ochoa Sanchez has been posted by Leo Giugiuc at the CutTheKnotMath facebook page, along with his and Dan Sitaru's solution (Solution 1).
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575387
