A Property of Angle Bisectors
What Is This About?
Problem
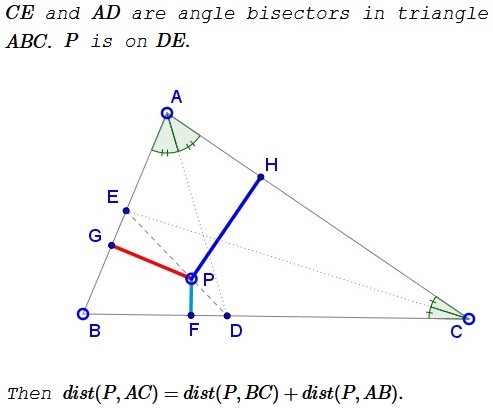
Solution 1
First, $P=kD+(1-k)E,$ $0\le k\le 1.$ Further, $\displaystyle D=\frac{bB+cC}{b+c}$ and $\displaystyle E=\frac{aA+bB}{a+b}.$ It follows that
$\displaystyle P=\left[\frac{1-k}{a+b}\right]aA+\left[\frac{1-k}{a+b}+\frac{k}{b+c}\right]bB+\left[\frac{k}{b+c}\right]cC.$
On the other hand,
$\displaystyle P=\left(\frac{x}{x+y+z}\right)A+\left(\frac{y}{x+y+z}\right)B+\left(\frac{z}{x+y+z}\right)C,$
where $x=2[\Delta PBC],$ $y=2[\Delta PCA],$ $z=2[\Delta PAB].$ Comparing the two identities,
$\displaystyle \left[\frac{1-k}{a+b}\right]a=\frac{a\cdot PF}{x+y+z},$
whence $\displaystyle PF=(x+y+z)\left[\frac{1-k}{a+b}\right].$ Similarly, $\displaystyle PG=(x+y+z)\left[\frac{k}{b+c}\right]$ and
$\displaystyle PH=(x+y+z)\left[\frac{1-k}{a+b}\right]+(x+y+z)\left[\frac{k}{b+c}\right],$
implying $dist(P, BC)=PH=PF+PG=dist(P,BC)+dist(P,AB).$
Solution 2
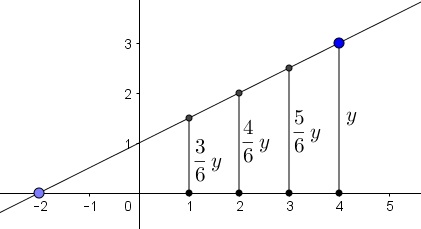
The distance to a line from a point on another line is a linear function just because an equation of a straight line is linear. This becomes clear if you consider one of the lines as, say, $x-\text{axis}:$
Next observe the extreme cases, where $P$ coincides with either $D$ or $E.$ Then, since the points on the angle bisector are equidistant from the sides of the angle, $DQ=dist(D,AC)=dist(D,AB)=DR$ and $ES=dist(E,BC)=dist(B,AC)=ET.$
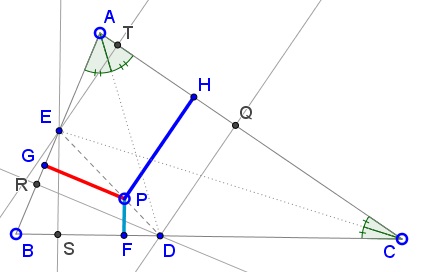
If $P=kD+(1-k)E,$ then $H=kQ+(1-k)T$ and $PH=kDQ+(1=k)ET.$
In a simialr fashion, or from the presence of two pairs of similar triangles: $EDR,EPG$ and $ESD,PFD,$ $PG=kDR=kDQ$ and $PF=(1-k)ES=(1-k)ET.$ Putting everything together,$PG+PF=kDQ+(1-k)ET=PH.$
Acknowledgment
Leo Giugiuc has kindly communicated to me this problem, along with his solution (Solution 1). The problem is from the RMT Magazine, Timisoara, Romania.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574373
