Problem 4160 from the Crux Mathematicorum
Problem

Solution
As we know, $D,E,F$ lie on the circumcircle $(ABC).$ Furthermore, we have angle distribution as shown below.
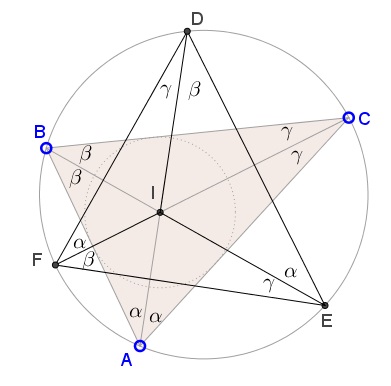
$[\Delta ABC]=2R^2\sin(2\alpha)\sin(2\beta)\sin(2\gamma),\\ [\Delta DEF]=2R^2\sin(\beta+\gamma)\sin(\gamma+\alpha)\sin(\alpha+\beta)=2R^2\cos\alpha\cos\beta\cos\gamma.$
It is also well known that
$r=4R\sin\alpha\sin\beta\sin\gamma.$
Combining everything,
$\displaystyle \begin{align} \frac{[\Delta DEF]}{[\Delta ABC]}&=\frac{2R^2\cos\alpha\cos\beta\cos\gamma}{2R^2\sin(2\alpha)\sin(2\beta)\sin(2\gamma)}\\ &=\frac{1}{8\sin\alpha\sin\beta\sin\gamma}=\frac{R}{2r}. \end{align}$
Acknowledgment
This is problem 4160 from the Crux Mathematicorum (Vol. 42(6), June 2016.) I am grateful to Leo Guigiuc who co-authored this problem with Marian Cucoanes. Leo has kindly pointed me to the problem and sent me their solution.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573882
