Prasolov's Pythagorean Identity
Source
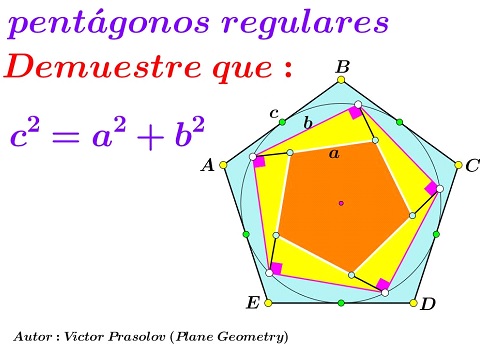
Problem
Pentagon $\beta\;$ is inscribed into the incircle of the pentagon $\gamma.\;$ Pentagon $\alpha\;$ is formed by the perpendiculars to the sides of $beta\;$ at the vertices. Their side length are $a,b,c,\;$ respectively.
Prove that
$a^2+b^2=c^2.$
Solution 1
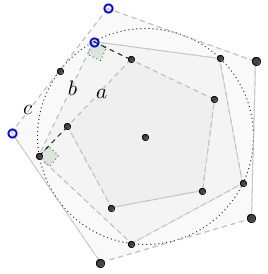
Below we shall refer to the following diagram:

Let, WLOG, the inradius of $ABCD\;$ equal $1.\;$ So $\displaystyle a=AB=2\tan\frac{\pi}{5}\;$ and $\displaystyle b=UV=2\sin\frac{\pi}{5}.\;$ Choose, $U=1,\;$ $V=u,\;$ $W=u^2,\;$ $T=u^3,\;$ $Z=u^4,\;$ where $\displaystyle u=\cos\frac{2\pi}{5}+i\sin\frac{2\pi}{5}.$
Evidently, there is a real number $k\;$ with
$\begin{cases} kR+(1-k)M &= 1\\ kM+(1-k)N &= u\\ kN+(1-k)P &= u^2\\ kP+(1-k)Q &= u^3\\ kQ+(1-k)R &= u^4. \end{cases}$
From these, $\displaystyle R=\frac{1}{k+(1-k)u}\;$ and $\displaystyle M=\frac{u}{k+(1-k)u}\;$ (see the reference.)
But $RM\perp VU,\;$ implying $\displaystyle\frac{R-M}{V-U}=ia.\;$ Thus, $\displaystyle\frac{1}{k+(1-k)u}=ia,\;$ and, from here, $k+(1-k)u^4=ia,\;$ so that $\displaystyle k=(1-k)\cos\frac{2\pi}{5},\;$ $\displaystyle c=\frac{1}{1-k}\frac{1}{\displaystyle\cos\frac{\pi}{5}}=2\tan\frac{\pi}{5}\sin\frac{\pi}{5}.\;$ But then $\displaystyle a^2+b^2=\left(2\tan\frac{\pi}{5}\right)^2=a^2.$
Solution 2
As before, assume the inradius of $\gamma\;$ - which is the circumradius of $\beta\;$ - equals $1.\;$ Let's $R\;$ be the circumradius of $\gamma,\;$ $r\;$ that of $\alpha.\;$ The required identity is equivalent to $r^2+1=R^2.$
We'll prove a general result suggested by Leo Giugiuc, viz., that the above holds for $n$-gons, with $n\ge 5.$
First off, $\displaystyle R=\frac{1}{\displaystyle\cos\frac{\pi}{n}}.$
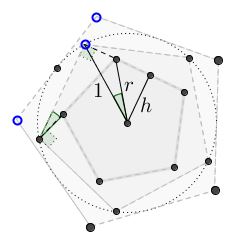
We see that
$\displaystyle\begin{align} h&=\cos\left(\frac{\pi (n-2)}{n}-\frac{\pi}{2}+\frac{\pi}{n}\right)\\ &=\cos\left(\frac{\pi (n-2)}{2n}\right)\\ &=\cos\left(\frac{\pi}{2}-\frac{\pi}{n}\right)\\ &=\sin\left(\frac{\pi}{n}\right). \end{align}$
Obviously, $\displaystyle r=\frac{h}{\displaystyle \cos\frac{\pi}{n}}=\tan\frac{\pi}{n}.\;$ From which $R^2=1+r^2,\;$ as required.
(Why are the two marked angles equal? Because the perpendiculars to the sides of $\beta\;$ induce a spiral similarity, the rotation part of which is by the angle between the sides.)
Acknowledgment
The problem and a proof (Proof 1) have been communicated to me by Leo Giugiuc, who also made an observation that the problem holds for all $n$-gons with $n\ge 5.$ It is my understanding that Leo found the problem at the Peru Geometrico forum where it was posted by Miguel Ocho Sanchez. The latter credits the problem to Victor Prasolov.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1966-2016 Alexander Bogomolny73580631
