Point between Two Roads
What Might This Be About?
Problem

Solution
A proof (almost) without words for finding the point $A$ for the minimal perimeter:
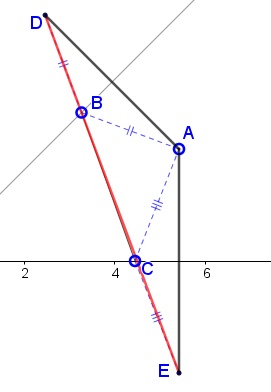
$D$ is the reflection of $A$ in the diagonal, $E$ the reflection of $A$ in the axis. $DE$ crosses the diagonal at $B'$ and the axis at $C'.$ The problem will be solved if $B'=B$ and $C'=C.$
Indeed, otherwise, for the perimeter $p$ of $\Delta ABC$ we have
$\begin{align} p &= BA+CA+AB = BD+CE+BC\\ &\ge DE \end{align}$
and the minimum is attained with $B,C\in DE.$
Now observe that if $A=(a,b),$ then $D=(b,a)$ and $E=(a,-b).$ In the minimal case, $p=DE=\sqrt{(b-a)^2+(b+a)^2}=\sqrt{2(a^2+b^2)}.$
Remark
There are two ways to use the applet to gain the insight into the problem. One which is suggested by the solution is to shift the points $B$ and $C$ to the position where they fall on $DE.$
The second one is reflect the line $BC$ in the diagonal and the axis and find the point $A'$ of intersection of the two reflections. When, by shifting $B$ and $C,$ $A'$ is made to coincide with $A,$ both $B$ and $C$ will lie on $DE.$
Acknowledgment
The problem was submitted by Kadir Altintas to the to Olimpiada pe Scoala (The School Yard Olympiad) facebook group and kindly communicated to me by Leo Giugiuc, along with a solution of his. (I have modified both just a little.)
![]()
|Contact| |Front page| |Contents| |Geometry| |Triangle constructions|
Copyright © 1996-2018 Alexander Bogomolny73574924
