Parallelogram in Parallelogram And in Projection
What Might This Be About?
Problem
Let $ABCD$ be a parallelogram; $E\in AC, IG, FH$ and $IG\parallel AB\parallel CD,$ $FH\parallel BC\parallel AD.$
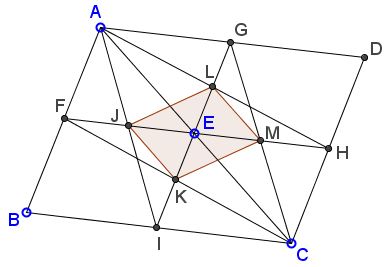
Then
$KJLM$ is a parallelogram.
If $ABCD$ is a rectangle, $KJLM$ is a rhombus
If $ABCD$ is a square, so is $KJLM.$
Solution
$AFCH$ is a trapezoid, hence $KL,$ the parallel to bases passing through $E$ has $E$ as midpoint. Similarly for the trapezoid $GAIC.$ This proves #1.
If $ABCD$ is a rectangle, the diagonals of the parallelogram $JKML$ are perpendicular, so it is a rhombus.
If $ABCD$ is a square, just see that $AFCH$ and $AGCI$ are symmetrical of each other about $AC.$
Projective Generalization
$ABCD$ is arbitrary quadrilateral. $X \equiv AB \cap CD,$ $Y \equiv BC \cap DA.$ $E$ is arbitrary point on $AC.$ $EX$ cuts $BC,DA$ at $I,G$ and $EY$ cuts $AB,CD$ at $F,H.$ $J \equiv AI \cap FH,$ $K \equiv CF \cap IG,$ $M \equiv CG \cap FH,$ $L \equiv AH \cap IG.$ Then $KM,LJ,BD,XY$ concur and $JK,ML,AC,XY$ concur.

Proof of the Generalization
Let $P \equiv XY \cap BD.$ Consider the involutive homology that fixes the the line pencil $P,$ the line $AC$ and that carries $B \mapsto D.$ Thus since $EX \mapsto EY,$ it follows that $I \mapsto H$ and $F \mapsto G,$ implying $CF \mapsto CG,$ $AI \mapsto AH$ so that $K \mapsto M$ and $J \mapsto L.$ Thus, $KM,LJ,BD,XY$ concur at $P$ and $JK,ML,AC,XY$ concur.
It needs to be observed that the two statements are in fact equivalent. It is clear that the latter implies the former. To prove the opposite direction, take $XY$ as a line at infinity.
Acknowledgment
The problem has been posted by Oai Thanh Dào at the CutTheKnotMath facebook page. The above solution is by Stan Fulger can be found in the comments that followed. Stan also added the generalization and its proof.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580756
