Parallel Lines in Rhombus
What Is This About?
Source

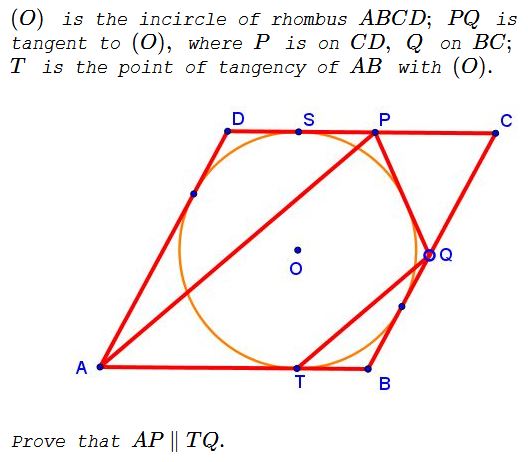
Problem
Solution
Let $PQ=y+z,\,$ $CQ=x+z,\,$ $CP=x+y.\,$ Then $(O)\,$ is the $C\text{-excircle}\,$ of $\Delta CPQ.\,$ Assume $(O)\,$ touches $CP\,$ at $S.\,$ Then
$\displaystyle \overrightarrow{CS}=\frac{(x+y+z)\overrightarrow{CP}}{x+y}\,$ and $\displaystyle \overrightarrow{CO}=\frac{(x+z)\overrightarrow{CP}+(x+y)\overrightarrow{CQ}}{2x}$
from which $\displaystyle \overrightarrow{CA}=\frac{(x+z)\overrightarrow{CP}+(x+y)\overrightarrow{CQ}}{x}.$
But $\overrightarrow{AT}=-\overrightarrow{CS},\,$ so that $\overrightarrow{AC}+\overrightarrow{CT}=-\overrightarrow{CS},\,$ $\overrightarrow{CT}=\overrightarrow{CA}-\overrightarrow{CS},\,$ $\overrightarrow{CQ}+\overrightarrow{QT}=\overrightarrow{CA}-\overrightarrow{CS},$
$\displaystyle \begin{align} \overrightarrow{QT}&=\overrightarrow{CA}-\overrightarrow{CS}-\overrightarrow{CQ}\\ &=\frac{(x+z)\overrightarrow{CP}+(x+y)\overrightarrow{CQ}}{x}-\frac{(x+y+z)\overrightarrow{CP}}{x+y}-\overrightarrow{CQ}, \end{align}$
which simplifies to $\displaystyle \overrightarrow{QT}=\frac{y}{x(x+y)}\cdot [z\overrightarrow{CP}+(x+y)\overrightarrow{CQ}].$
On the other hand,
$\displaystyle\begin{align} \overrightarrow{PA}&=\overrightarrow{CA}-\overrightarrow{CP}\\ &=\frac{(x+z)\overrightarrow{CP}+(x+y)\overrightarrow{CQ}}{x}-\overrightarrow{CP}\\ &=\frac{1}{x}\cdot[z\overrightarrow{CP}+(x+y)\overrightarrow{CQ}] \end{align}$
which, in particular, proves the claim: $QT\parallel AP.$
Acknowledgment
This problem has been kindly communicated to me by Leo Giugiuc, along with his solution. The problem by Rubén Auqui (Dario) was originally posted at the Peru Geometrico facebook group.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73570441
