Mixing Incenter And Orthocenter in Greece
Problem
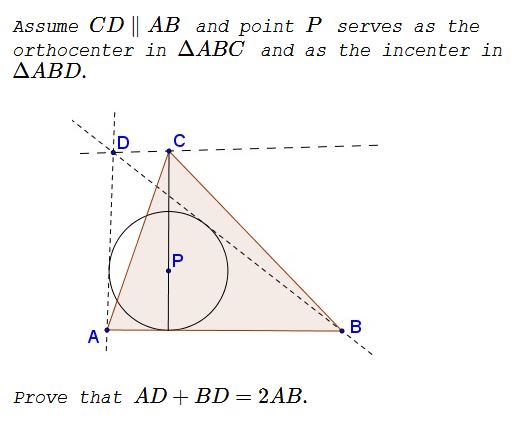
Solution
Let $A=(-a,-1),\,$ $B=(b,-1),\,$ $P=(0,0).\,$ Then $D=\displaystyle \left(\frac{a-b}{ab-1},\frac{ab+1}{ab-1}\right),\,$ where $a,b\gt 0\,$ and $ab\gt 1.$ (This is because the slope of $BP=\displaystyle -\frac{1}{b},\,$ so that the slope of $\displaystyle DB=-\frac{2b}{b^2-1}\,$ and, similarly, the slope of $\displaystyle DA=\frac{2a}{a^2-1},\,$ which supplies two equations for finding the coordinates of $D.)\,$
Since $P(0,0)\,$ is the orthocenter of $\Delta ABC\,$ and $CD\parallel AB,\,$ we deduce that $\displaystyle C=\left(0,\frac{ab+1}{ab-1}\right).\,$
Now, on one hand, the slope of $BC\,$ is $\displaystyle -\frac{2a}{ab-1}.\,$ On the other hand, since $BC\,$ is perpendicular to $AP,\,$ whose slope is $\displaystyle \frac{1}{a},\,$ the slope of $BC\,$ is equal to $-a.\,$ Equating the two values, $\displaystyle -\frac{2a}{ab-1}=-a,\,$ leads to $ab=3.$
With $ab=3\,$ $C=(0,2),\,$ such that the altitude from $C\,$ equals $3.\,$ Thus we find the area $[\Delta ABC]=\displaystyle \frac{3}{2}BC.\,$ On the other hand, $[\Delta ABC]=[\Delta ABD]\,$ yields
$\displaystyle \frac{3}{2}AB=\frac{1}{2}(AD+BD+AB)\cdot 1,$
which implies $AD+BD=2\cdot AB.$
Acknowledgment
This problem has been kindly posted by Thanos Kalogerakis (Greece) at the CutTheKnotMath facebook page. The above solution is by Leo Giugiuc. I am grateful to Leo for holding my hand while writing up this page.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73550236
