Chasing Angles Among Angle Bisectors

Problem

In a cyclic quadrilateral $ABCD,$ with $O$ as a circumcenter, let $F$ and $G$ be the midpoints of sides $AB$ and $AD,$ respectively.

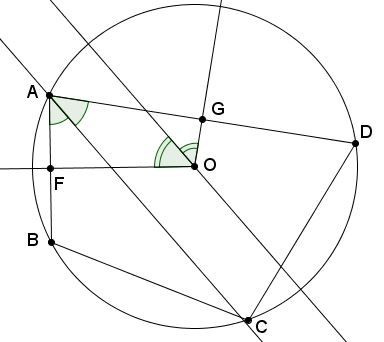
parallel angle bisectors - problem

Prove that the bisectors of angles $BAD$ and $FOG$ are parallel.

Proof

The proof is by straightforward angle chasing.

Since $OF\perp AB$ and $OG\perp AD$ the quadrilateral $ABOD$ is cyclic. Let $K$ be its circumcenter and define $L$ and $M$ as the intersection of its circumcircle $(K)$ with the given angles bisectors. $OK$ serves as a diameter of $(K).$

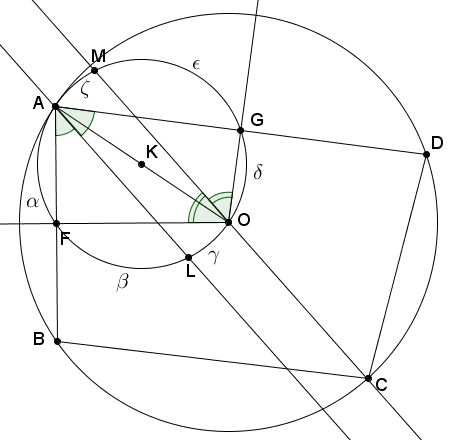
parallel angle bisectors - solution

In the above diagram circle $(K)$ is divided into six arcs, with angle measurements $\alpha,$ $\beta,$ $\gamma,$ $\delta,$ $\epsilon,$ $\zeta$ that satisfy the following conditions:

$\begin{align} (1) & \alpha +\beta +\gamma = \delta +\epsilon +\zeta = 180^{\circ},\\ (2) & \beta =\gamma +\delta,\\ (3) & \epsilon = \alpha +\zeta. \end{align}$

We want to prove that $\gamma = \zeta.$ This is achieved by substituting (2) and (3) into (1):

$\alpha + (\gamma +\delta )+\gamma = \delta + (\alpha +\zeta )+\zeta,$

which reduces to $2\gamma = 2\zeta,$ and the assertion follows.

Note: the statement could have been formulated for the triangle $ABD$ as $C$ plays no role in either the formulation of the proof. The reason for the above choice is merely historical.

71536310