An Unexpected Pair of Similar Triangles Which Are Equal
What is this about?
Problem
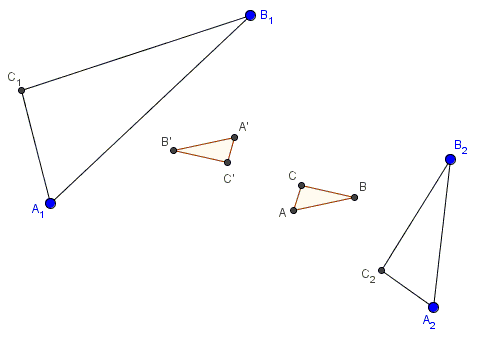
Given two similar triangles $A_{1}B_{1}C_{1}$ and $A_{2}B_{2}C_{2}.$
The centroids of the triangles $A_{1}B_{2}C_{2},$ $A_{2}B_{1}C_{2},$ and $A_{2}B_{2}C_{1}$ form a similar triangle $ABC$.
The centroids of the triangles $A_{2}B_{1}C_{1},$ $A_{1}B_{2}C_{1},$ and $A_{1}B_{1}C_{2}$ form a similar triangle $A'B'C'$.
Triangles $ABC$ and $A'B'C'$ are centrally symmetric in the centroid $(\alpha_1+\beta_1+\gamma_1+\alpha_2+\beta_2+\gamma_2)/6$ of the six given vertices.
Hint
As in several similar problems, complex numbers show the clearest way to achieve the goal.
Solution

I associate indexed complex numbers $\alpha$ with corresponding $A$ vertices, $\beta$ with $B,$ and $\gamma$ with $C$. Let $d$ be a complex number that defines the shape of the given triangles $A_1B_1C_1$ and $A_2B_2C_2$ in the following sense:
$\gamma_1=\alpha_1+d(\beta_1-\alpha_1)$ and
$\gamma_2=\alpha_2+d(\beta_2-\alpha_2).$
We also have
$\alpha=(\alpha_1+\beta_2+\gamma_2)/3,$
$\beta=(\alpha_2+\beta_1+\gamma_2)/3,$
$\gamma=(\alpha_2+\beta_2+\gamma_1)/3,$
${\alpha}'=(\alpha_2+\beta_1+\gamma_1)/3,$
${\beta}'=(\alpha_1+\beta_2+\gamma_1)/3,$
${\gamma}'=(\alpha_1+\beta_1+\gamma_2)/3.$
First, we prove Dao Thanh Oai's unexpected observation that $\gamma=\alpha+d(\beta-\alpha).$ Check that
\( \begin{align} \gamma &= (\alpha_2+\beta_2+\gamma_1)/3 \\ &= (\alpha_2+\beta_2+\alpha_1+d(\beta_1-\alpha_1))/3 \end{align} \)
while
\( \begin{align} \alpha+d(\beta-\alpha) &= (\alpha_1+\beta_2+\gamma_2)/3 \\ &\space\space\space+ d[(\alpha_2+\beta_1+\gamma_2)/3-(\alpha_1+\beta_2+\gamma_2)/3] \\ &= (\alpha_1+\beta_2+\alpha_2+d(\beta_2-\alpha_2+\alpha_2+\beta_1-\alpha_1-\beta_2))/3 \\ &= (\alpha_1+\beta_2+\alpha_2+d(\beta_1-\alpha_1))/3. \end{align} \)
Hence, $\gamma=\alpha+d(\beta-\alpha),$ making $\Delta ABC$ similar to the given two triangles. Obviously, in the same manner we can show that $\Delta A'B'C'$ is also similar to the given two.
Now, let's find the midpoints of segments $AA',$ $BB',$ and $CC'.$ Say,
$ \begin{align} (\alpha+{\alpha}')/2&=[(\alpha_1+\beta_2+\gamma_2)/3+(\alpha_2+\beta_1+\gamma_1)/3]/2 \\ &=(\alpha_1+\beta_1+\gamma_1+\alpha_2+\beta_2+\gamma_2)/6. \end{align} $
Similarly,
$(\beta+{\beta}')/2=(\alpha_1+\beta_1+\gamma_1+\alpha_2+\beta_2+\gamma_2)/6$ and
$(\gamma+{\gamma}')/2=(\alpha_1+\beta_1+\gamma_1+\alpha_2+\beta_2+\gamma_2)/6,$
making triangles $ABC$ and $A'B'C'$ centrally symmetric and, hence, equal.
Acknowledgment
Dao Thanh Oai has defined and proved in a post at the CutTheKnotMath facebook page that $\Delta ABC$ defined above is similar to triangles $A_1B_1C_1$ and $A_2B_2C_2.$ It was just one extra step to reverse the indices $1\leftrightarrow 2\space.$
P.S.
Dao Thanh Oai has observed that the centroids of the four triangles and the six vertices are collinear. For example,
$(\alpha+\beta+\gamma)/3=[(\alpha_1+\beta_1+\gamma_1)+2(\alpha_2+\beta_2+\gamma_2)]/3.$
Similarly,
$({\alpha}'+{\beta}'+{\gamma}')/3=[2(\alpha_1+\beta_1+\gamma_1)+(\alpha_2+\beta_2+\gamma_2)]/3.$
Thus, if we denote the centroids of $A_1B_1C_1,$ $A'B'C',$ $ABC,$ and $A_2B_2C_2$ as, respectively, $K_1,$ $K',$ $K,$ and $K_2,$ the points are indeed collinear and are always located in the following sequence:
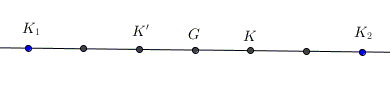
Points $K_1,$ $K',$ $K,$ and $K_2,$ are equally spaced, while $G$ is the midpoint of two pairs of points: $K_1,$ $K_2,$ and $K',$ $K.$
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578900
