Miguel's Special Trapezoid
Source
The problem below has been stated by Miguel Ochoa Sanchez:
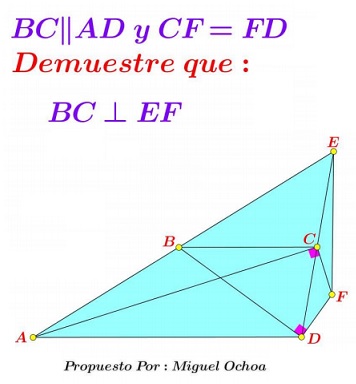
Problem
In the trapezoid $ABCD,\;$ $BC\parallel AD\;$ and $CF\perp AC,\;$ $DF\perp BD.\;$ Also, $E=AB\cap CD.$
Prove that $CF=DF\;$ iff $BC\perp EF.$
Proof
Choose $A=(-2a,0),\;$ $B=(0,2),\;$ $C=(2c,2),\;$ and $D(2d,0).\;$ With these, we can find the equations of several lines:
$\begin{cases} CF: & (a+c)x+y = 2c^2+2ac +2,\\ DF: & dx-y=2d^2,\\ CD's\;bisector: & (d-c)x-y=d^2-c^2-1,\\ AE: & x-ay=-2a,\\ DE: & x+(d-c)y=2d. \end{cases}$
The condition for the three to be concurrent (at $F)\;$ is $\left|\begin{array}{ccc}a+c&1&2c^2+2ac+2\\d&-1&2d^2\\d-c&-1&d^2-c^2-1\end{array}\right|=0,\;$ from which
(*)
$\displaystyle a=\frac{(c-d)(d^2+c^2+1)}{d^2-c^2-1}.$
Solving the equations for $DF\;$ and the bisector of $CD\;$ gives $\displaystyle x_F=\frac{d^2+c^2+1}{c},\;$ meaning that the equation of the perpendicular to $BC\;$ through $F\;$ is $\displaystyle x=\frac{d^2+c^2+1}{c}.\;$ For it to be concurrent with $AE\;$ and $DE\;$ we need $\left|\begin{array}{ccc}1&0&\displaystyle\frac{b^2+c^2+1}{c}\\1d&d-c&2d\\1&-a&-2a\end{array}\right|=0,\;$ which also yields (*), and this leads to $x_E=x_F.$
Acknowledgment
The original statement and the proof have been emailed to me by Leo Giugiuc with credits to Miguel Ochoa Sanchez. I thank them both.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1966-2016 Alexander Bogomolny73582542
