Miguel Ochoa's Chords And Tangents

What Might This Be About?

Source

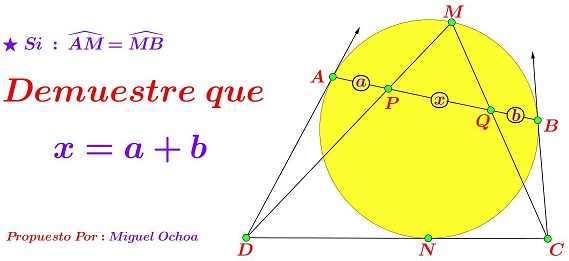
Miguel Ochoa's chords and tangents, source

Problem

Lines $AD,CB,CD\;$ are tangent to a given circle at $A,\;$ $B,\;$ and $N,\;$ respectively. $M\;$ is the midpoint of the arc $AB\;$ opposite $N;\;$ $P=AB\cap DM,\;$ $Q=AB\cap CM.\;$

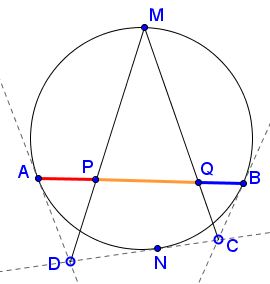
Miguel Ochoa's chords and tangents, problem

Prove that $PQ=AP+BQ.$

Proof

Draw a tangent to the circle at $M\;$ and let it intersect $AD\;$ in $E\;$ and $BC\;$ in $F.$

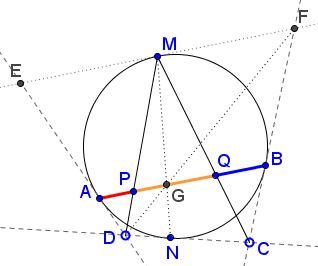
Miguel Ochoa's chords and tangents, solution

According to a theorem often attributed to Newton, lines $AB,\;$ $MN,\;$ $DF,\;$ and $CE\;$ are concurrent. Let $G\;$ be the point of concurrency. Then, since $EF\parallel AB,\;$ the trapezoid $ABFE\;$ is isosceles. In addition, since $M\;$ is the midpoint of arc $AB,\;$ $AE=EM=MF=FB.$

It follows that $AP=PG\;$ and, similarly, $GQ=BQ.\;$ Adding up proves the assertion.

Acknowledgment

The problem and the solution have been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page.

72104479