Concurrence on Angle Bisector

What Might This Be About?

Problem

In a coordinate system, not necessarily Cartesian, let $A=(0,a),$ $B=(b,0),$ $A^{+} = (h,a),$ $A^{-} = (-h,a),$ $B^{+} = (b,h),$ $B^{-} = (b,-h).$

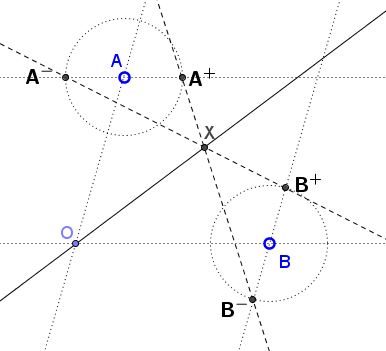
Concurrence on Angle Bisector - problem

Prove that the lines $A^{+}B^{-}$ and $A^{-}B^{+}$ meet on the bisector $y=x$ of angle $AOB.$

Solution

Let line $A^{-}B^{+}$ crosses $y=x$ in point $X=(x,x),$ as shown below. Note also the appearance of points $D$ and $E$ whose definition is clear from the diagram.

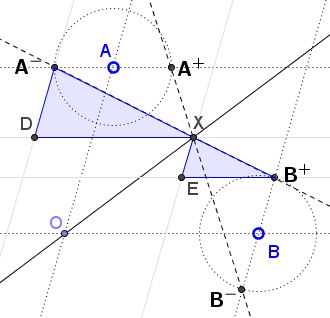
Concurrence on Angle Bisector - solution 1

From the similarity of triangles $ADX$ and $XEB,$ $\displaystyle\frac{A^{-}D}{DX}=\frac{XE}{EB^{+}}.$ In other words,

(1)

$\displaystyle\frac{a-x}{x+h}=\frac{x-h}{b-x}.$

Let $X'=(x',x')$ be the point where line $A^{+}B^{-}$ meets the bisector $y=x.$ We also add another pair of similar triangles, $A^{+}FX\;$ and $XGB^{-},$ as shown in the diagram below,

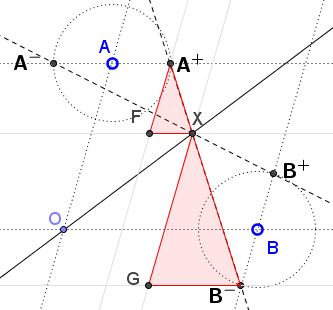
Concurrence on Angle Bisector - solution 2

This gives another proportion, $\displaystyle\frac{A^{+}F}{FX'}=\frac{X'G}{GB^{-}}.$ In other words,

(2)

$\displaystyle\frac{a-x'}{x'-h}=\frac{x'+h}{b-x'}.$

Obviously, (1) and (2) are one and the same equation, making $x=x'$ so that the lines $A^{+}B^{-}$ and $A^{-}B^{+}$ do indeed meet on the bisector $y=x.$

In vector form, again, the two equations for the location of the point on the bisector give the same result:

$\displaystyle\frac{a + h}{b + a} (b, h) + \frac{b - h}{b + a} (-h, a) = \frac{ba + h^2}{b + a} (1, 1)\\ \displaystyle\frac{a - h}{b + a} (b, -h) + \frac{b + h}{b + a} (h, a) = \frac{ba + h^2}{b + a} (1, 1),$

or, easily verifiable,

$ (ba + h) (b, h) + (ba - h) (-h, a) = (ba + h^2) (1, 1)\\ (ba - h) (b, -h) + (ba + h) (h, a) = (ba + h^2) (1, 1).$

Acknowledgment

The problem and its solution are by Grégoire Nicollier, University of Applied Sciences of Western Switzerland.

71946129