Concurrent and Parallel Lines in Parallelogram
What Might This Be About?
Problem
Through point $F$ on the diagonal $AC$ of parallelogram $ABCD$ draw to lines $EH$ and $GI$ where $E\in BC,$ $I\in CD,$ $H\in AD,$ $G\in AB.$
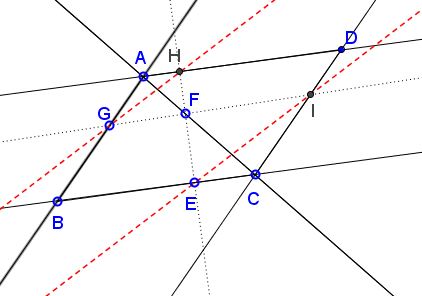
Prove that $GH\parallel EI.$
Solution
There is a good deal of similar triangles, e.g., $\Delta AHF\sim\Delta CEH,$ $\Delta AGF\sim\Delta CIF.$ From these we derive proportions:
$\displaystyle\frac{AH}{EC}=\frac{AF}{CF}=\frac{AG}{CI}.$
Now, since also $\angle BAD=\angle BCD,$ $\Delta AGH\sim\Delta CIE,$ implying that one is obtained from the other with a homothety centered at $F$ and the coefficient $\displaystyle -\frac{AF}{CF}.$ This insures that $GH$ and $EI$ are indeed parallel.
Acknowledgment
This problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580060
