A Median Surprise
What is this about?
Problem
Let $D,E,F$ be the midpoints of the sides of $\Delta ABC,$ as shown below. Rotate triangles $CDG, AEG, BFG$ $180^{\circ}$ around points $D,E,F,$ respectively, into triangles $BDG_{b}, CEG_{c}, AFG_{a}.$
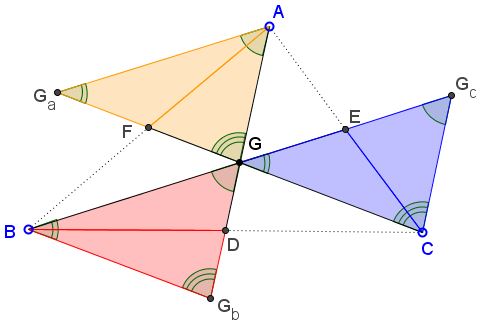
This procedure creates three congruent triangles: $AGG_{a},$ $BGG_{b},$ and $CGG_{c}.$
Acknowledgment
I learned of this statement by Lee Sallows and its extension by John Golden (@mathhombre) and Pat Ballew's from their tweets, google+ conversation and Pat's blog.
Proof
The proof is extremely simple and may be discerned by just viewing of the medians diagram:
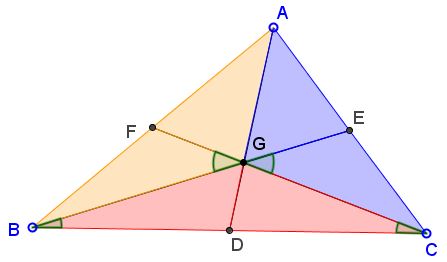
Say, $FG$ and $FG_a$ are collinear because the latter is just a reflection of the former in point $F.$
$\angle AG_{a}G=\angle BGF=\angle CGE=\angle CGG_{c}.$ In addition,
$\begin{align} \angle GBG_{b} &=\angle GBD+\angle DBG_{b}\\ &=\angle GBC+\angle DCB\\ &= 180^{\circ}-\angle BGC\\ &=\angle BGF. \end{align}$
Other angles are treated similarly. Finally,
$AG_{a} = BG = 2GE = GE+EG_{c}=GG_{c},$
making triangles $BDG_{b}, CEG_{c}, AFG_{a}$ not only similar but in fact congruent.
Extra
It was observed that if $\Delta ABC$ is equilateral or isosceles, so are the new ones. However, in the later case there is no similarity. I can add that the similarity between triangles $BDG_{b}, CEG_{c}, AFG_{a}$ and $\Delta ABC$ would imply that the latter (and the rest of them) are equilateral. However, John Golden and Pat Ballew made an additional discovery by inquiring of what happens if the same procedure was being applied to the new triangles. Their discovery is that the second generation of the triangles is similar to the original $\Delta ABC.$
This is illustrated in the following diagram:
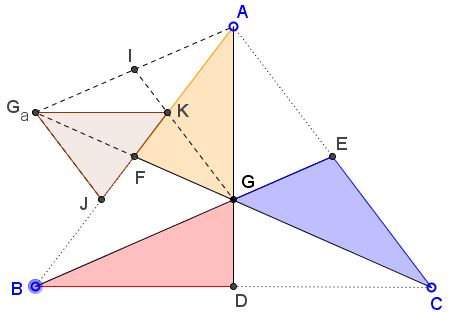
In the diagram $F$ serves as the center of spiral similarity with coefficient $\frac{1}{3}.$
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73574006
