Some Properties of Common Tangents

What is this about?

Problem

Let $HE$ and $FG$ be two internal tangents of non-overlapping circles $(A)$ and $(C),$ as shown below.

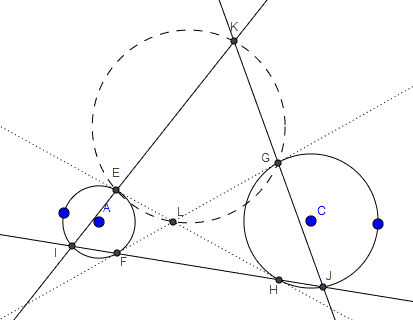
Properties of common tangents

Let $FH$ intersect the second time $(A)$ in $I$ and $(C)$ in $J.$ Define $L$ to be the intersection of $EH$ and $FG,$ $K$ the intersection of $EI$ and $GJ.$ Then

$FI=HJ,$
$\angle KIJ = \angle KJI,$
Points $E,L,G,K$ are concyclic.

Hint

Think of the Power of a Point theorem, and properties of inscribed angles.

Solution

Properties of common tangents

By the Power of a Point theorem, $FG^{2}=FH\cdot FJ$ and also $HE^{2}=HF\cdot HI.$ Then $HE=FG$ implies $FI=HJ.$

Since angles $ELF$ and $GLH$ are vertical and, hence, equal, the arcs subtended by chords $EF$ in $(A)$ and $GH$ in $(C)$ have the same angular measure, making central inscribed angles $GJH$ and $EIF$ equal such that $\angle KIJ = \angle KJI.$

Finally, since $FG$ and $EH$ are tangent to $(C),$ they are orthogonal to the radii of $(C)$ at the points of tangency. It follows that

$ \begin{align} \angle ELG &= 180^{\circ} -\angle GLH \\ &= \angle GCH \\ &= 2\angle GJH = 2\angle KJI. \end{align} $

On the other hand, $\angle IKJ=180^{\circ}-\angle KIJ-\angle KJI=180^{\circ}-2\angle KJI.$ Therefore, $\angle EKJ + \angle ELG=180^{\circ},$ making quadrilateral $ELJK$ cyclic.

Also

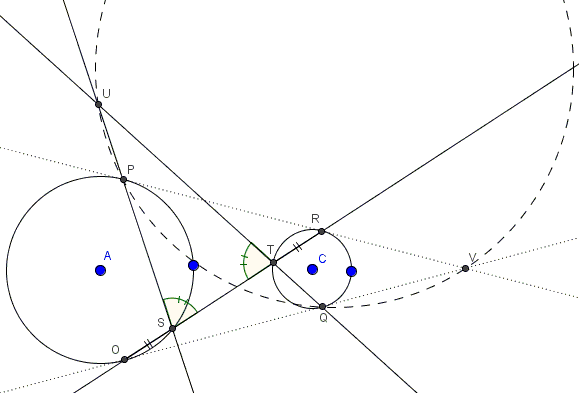
The two external tangents have similar properties:

Properties of common external tangents

Acknowledgment

The problem with solution has been posted by Emmanuel Antonio José García at the CutTheKnotMath facebook page.

71545042