Problem 1 from the 2006 IMO
Problem
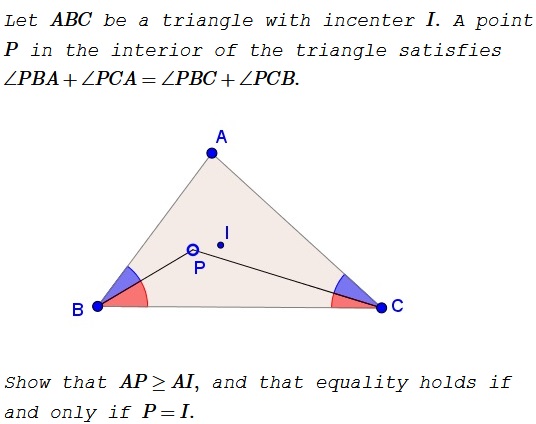
Solution
Let angles at $A,$ $B,$ $C$ be $2\alpha,$ $2\beta,$ $2\gamma,$ respectively. $\alpha+\beta+\gamma=90^{\circ}.$
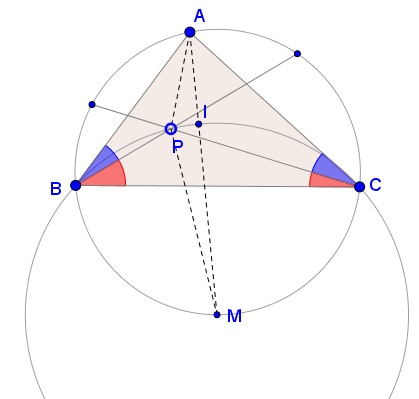
Note that
$\angle PBA + \angle PCA + \angle PBC + \angle PCB=2\beta+2\gamma=180^{\circ}-2\alpha.$
Thus, condition $\angle PBA + \angle PCA + \angle PBC + \angle PCB$ implies that
$\angle PBC + \angle PCB=90^{\circ}-\alpha$
so that $\angle BPC=90^{\circ}+\alpha,$ placing $P$ on the circumcircle $(BCI).$ As we know, $(BCI)$ is centered at the midpoint $M$ of the arc $\overset{\frown}{BC},$ opposite $A,$ meaning in part that $A,$ $I,$ $M$ are collinear and that $MP=MI.$
By the triangle inequality
$AP+MP\ge AM=AI+MI=AI+MP,$
from which $AP\ge AI$ with equality only when $P=I.$
Acknowledgment
I am grateful to Siyoun Sung for pointing out that this 2006 IMO problem has the elegant solution described above. Siyoun Sung has observed that the problem succumbs easily based on a property of the incircle. It's edifying to compare this proof with an older one.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574216
