Chain of Six Intersecting Circles

What Might This Be About?

Problem

Circles $(O_{i}),$ $i=1,\ldots,6,$ are drawn on the sides of the hexagon $A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}$ as diameters as shown below. There are additional intersection points, $B_{i},$ $i=1,\ldots,6.$

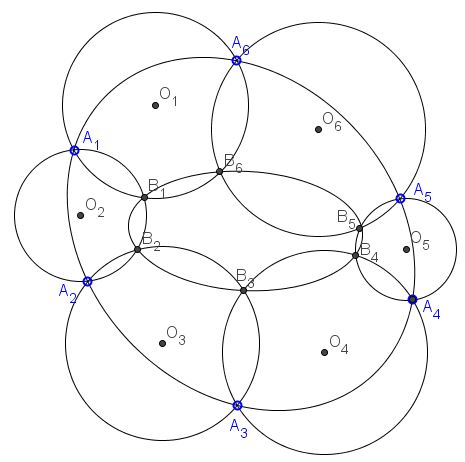
a chain of six intersecting circle - problem

Prove that, if points $A_{i},$ $i=1,\ldots,6,$ lie on a conic, then so are points $B_{i},$ $i=1,\ldots,6.$

Proof

proof is wanting

Acknowledgment

The claim above is an analogue of the statement about a four circles chain. It is slight modification and generalization of a statement posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.

Francisco Javier García Capitán has found a computer-verified solution in barycentric coordinates for the original problem of a hexagon inscribed in a circle.

71546988