From Perpendicular Center Lines to Concyclic Points

What Is This About?

Problem

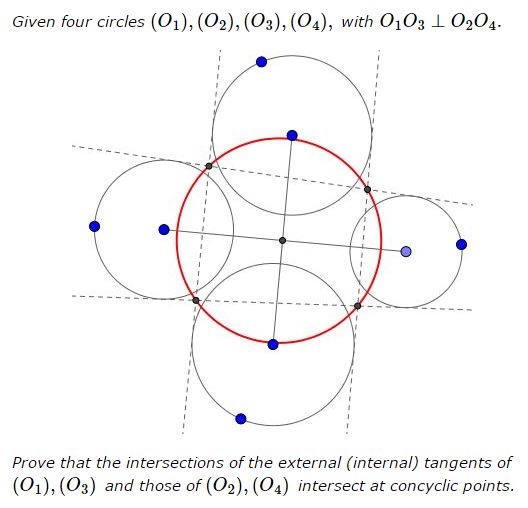
From Perpendicular Center Lines to Concyclic Points, problem

Solution

The problem is easily solved by angle chasing. Observe the presence of several cyclic quadrilaterals, e.g.,

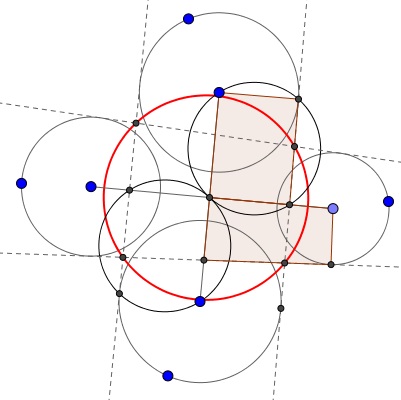
From Perpendicular Center Lines to Concyclic Points, example

This explains an interesting distribution of equal angles:

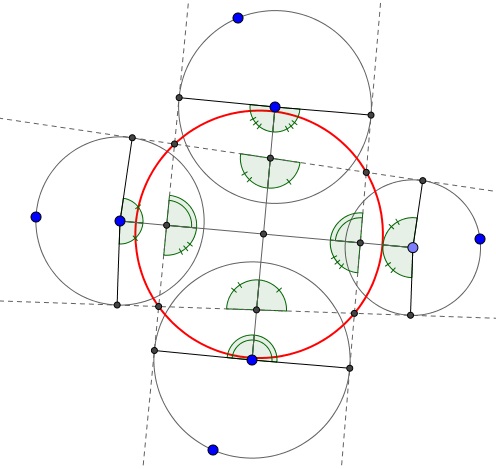
From Perpendicular Center Lines to Concyclic Points, proof

Recombining suitable angles we see that the opposite angles at the four points of tangent intersections do indeed add up to $180^{\circ},\,$ making the points concyclic.

Acknowledgment

The problem has been kindly posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

508 Resource Limit Is Reached

Resource Limit Is Reached

The website is temporarily unable to service your request as it exceeded resource limit. Please try again later.