Four Isosceles Triangles Hinged at Vertices

What is this about?

Problem

Triangles $BAB'$, $CAC',$ $BDC,$ and $BD'C'$ are similar and isosceles, with apex angles at $A,$ $D,$ and $D',$ respectively.

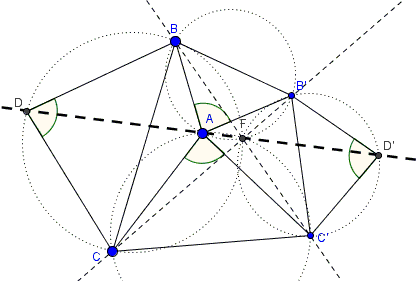
A configuration of four similar isosceles triangles - Problem

Prove that

$D,$ $A,$ and $D'$ are collinear. (Let $f$ be the line.)
$AD=AD'.$
$BC'$ and $B'C$ meet at point $F$ on $f.$
$BC'=B'C.$
The circumcircles of triangles $ABB',$ $ACC',$ $BCD,$ and $B'C'D'$ concur at $F.$

Hint

Rotation transform is bound to play an important role for this problem.

Solution

A product of successive rotations is either a rotation or a translation (which is a rotation through $0^{\circ}.$) In any event, the resulting angle of rotation equals the sum of all the rotations in the sequence.

Consider a sequence of rotations each through the apex angle of the given isosceles triangles:

Clockwise around $D;$
Counterclockwise around $A;$
Clockwise around $D';$
Counterclockwise around $A;$

A configuration of four similar isosceles triangles - solution, step 1

Since the angles add up to $0^{\circ},$ the resulting transform is at best a translation. But this translation maps $B$ to itself, implying that in fact it's an identity transform: it leaves the whole plane (point by point) in place. In particular, it leaves in place point $A.$ But the last rotation has $A$ as a fixed point anyway, so that the product of the first three already maps $A$ to itself. It follows that isosceles triangles $ADA'$ and $A''D'A$ are equal and, in particular, $AD=AD',$ proving #2.

... to be continued ...

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

72352981