Six Concyclic Circumcenters in Fermat's Configuration
What is this about?
Problem
The extended lines of three equal segments $AA',$ $BB',$ $CC'$ meet at point $F$ at $120^{\circ}$ to each other:
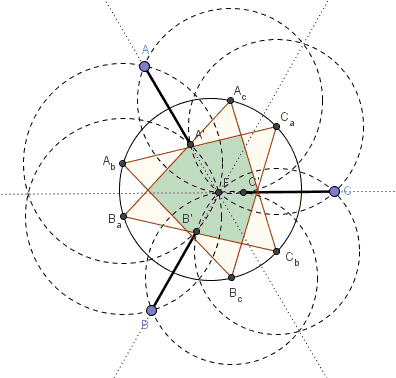
Prove that
The circumcenters $A_b,$ $A_c,$ $B_a,$ $B_c,$ $C_a,$ $C_b$ of $AB'F,$ $AC'F,$ $BA'F,$ $BC'F,$ $CA'F,$ $CB'F,$ respectively, are concyclic.
The two triangles $A_bB_cC_a$ and $A_cC_bB_a$ are equilateral.
Hint
One point to pay attention to is that there are three lines at $120^{\circ}$ or, if you wish, $60^{\circ}$ angles to each other. Another important point is that the three equal segments are all equal. Remember the construction of the circumcenter and circumcircle of a triangle.
Solution
The configuration features three pairs of equally spaced parallel lines.
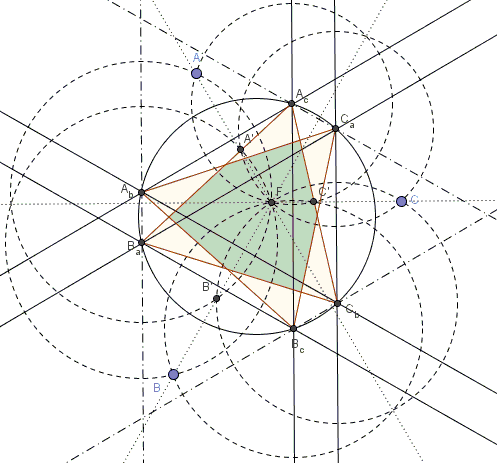
For examples, $AA'$ is the radical axis of $(A_b)$ and $(A_c)$ (because both pass through $F$ and $A$), $(C_a)$ and $(B_a)$ (because both pass through $F$ and $A'.$) It follows that $A_bA_c\perp AF,$ while $B_aC_a\perp A'F$ such that $A_bA_c\parallel B_aC_a.$ Furthermore, the distance between $A_bA_c$ and $B_aC_a$ is exactly $AA'/2.$
The lines are inclined $60^{\circ}$ to each other because they are perpendicular to the given three lines. Being equally spaced, the three pairs of lines produce a pattern which is both mirror and rotationally symmetric, such that the six circumcenters are indeed concyclic. By symmetry, or because all six chords subtend equal angles the chords form three equilateral triangles.
In addition, also due to the symmetry of the configuration, $B_cC_b\perp AA',$ implying that $AA'$ passing through $F$ - a common point of $(B_c)$ and $(C_b)$ - and being perpendicular to $B_cC_b$ is necessarily the radical axis of $(B_c)$ and $(C_b).$
Finally, the three lines $AbB_a,$ $B_cC_b,$ and $A_CC_a$ also form an equilateral triangle.
Acknowledgment
The problem and the proof are from the online document by Dao Thanh Oai who posted an announcement at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573073
