Excircles in Trapezoid
What Is This About?
Problem
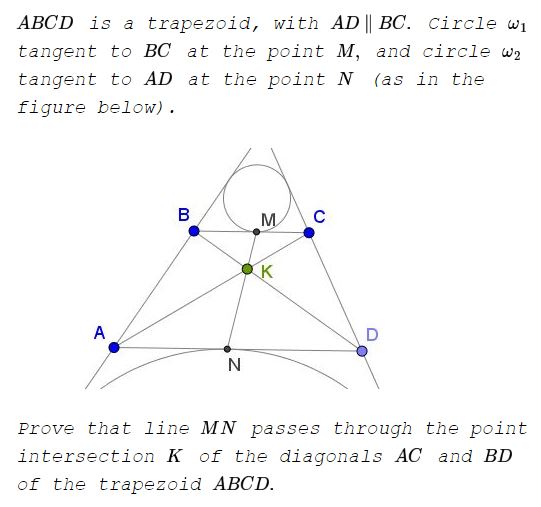
Solution 1
Let's $A'\,$ be the intersection of $AB\,$ and $CD.\,$ WLOG, we may assume that the configuration is as shown below:
Triangles $ADA'\,$ and $BCA'\,$ are similar such that, say, $\displaystyle \frac{AD}{BC}=\frac{AA'}{BA'}=\frac{DA'}{CA'}.\,$ Denote this ration $\lambda.\,$ If $s\,$ and $s'\,$ are the semiperimeters of triangles $ADA'\,$ and $BCA'\,$ then we also have $\displaystyle \frac{s}{s'}=\lambda.$
Note that $\omega_1\,$ is the incircle while $\omega_2\,$ the excircle of $\Delta BCA'.\,$ It is known that , say, $CM=s'-BA'\,$ whereas $AN=s-AA'\,$ such that $\displaystyle \frac{AN}{CM}=\frac{s-AA'}{s'-BA'}=\frac{\lambda\cdot s'-\lambda\cdot BA'}{s'-BA'}=\lambda.\,$ Since triangles $ADK\,$ and $CBK\,$ are similar, they are obtained from each other with a spiral similarity around point $K.\,$ Points $M\,$ and $N\,$ correspond to each other under that transformation, implying that the line joining the two passes through the center of the transformation.
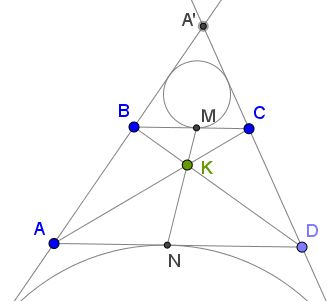
A similar argument applies to the case where the circle are drawn on the other sides of the trapezoid bases:
In the special case where the trapezoid degenerates into parallelogram, the spiral similarity becomes a reflection in $K\,$ and the argument simplifies.
Solution 2
Let $\angle BAD = 2\alpha$, $\angle CDA = 2\beta$, the height of the trapezoid $=h$, the radius of the circle touching $BC=r$, the radius of the circle toucing $AD=R$ and the $X$ axis point from $A$ to $D$. Thus,
$\begin{align} \vec{AB}&\,= h\cot 2\alpha\hat{x}+h\hat{y} \\ \vec{AM}&\,= \vec{AB}+\vec{BM}=(h\cot 2\alpha+r\cot\alpha)\hat{x}+h\hat{y} \\ \vec{AC}&\,= \vec{AM}+\vec{MC}=(h\cot 2\alpha+r\cot\alpha+r\cot\beta)\hat{x}+h\hat{y} \\ \vec{AN}&\,= R\cot\left(\frac{\pi}{2}-\alpha\right)\hat{x}=R\tan\alpha\hat{x} \end{align}$
Let $\vec{AK}=k\vec{AC}$ for some $k$. From similarity of triangles $KCB\,$ and $KAD,$
$\displaystyle \frac{k}{1-k}=\frac{|\vec{AD}|}{|\vec{BC}|}=\frac{R(\tan\alpha + \tan\beta)}{r(\cot\alpha +\cot\beta)}=\frac{R}{r}\tan\alpha\tan\beta.$
Note,
$\displaystyle \frac{k}{1-k}\vec{MC}=\left(\frac{R}{r}\tan\alpha\tan\beta\right)r\cot\beta\hat{x}=R\tan\alpha\hat{x}=\vec{AN}.$
Thus,
$\vec{AK}=k\vec{AC}=k\vec{AM}+k\vec{MC}=k\vec{AM}+(1-k)\vec{AN}.$
Hence, $K$ lies on $MN$.
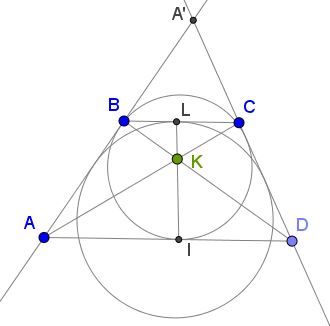
Solution 3
Homothety of center $A',\,$ the intersection point of $BA\,$ and $CD,\,$ which sends $BC\,$ to $AD,\,$ also sends the inscribed circle $omega_1\,$ of $\Delta OBC,\,$ to the inscribed circle of $\Delta A'AD,\,$ of which circle $\omega_2\,$ is an excircle. If $M\,$ maps to $M',\,$ from the homothety we have $\displaystyle \frac{BM}{MC} =\frac{AM'}{M'D}.\,$ But $AM'=DN,\,$ $M'D=AN,\,$ thus $\displaystyle \frac{BM}{MC}=\frac{DN}{NA},\,$ etc., using the following
LEMMA
- Three (or more) concurrent lines divide any two parallel lines in segments with the same ratio.
- Converse: Three (or more) non parallel lines, which divide two parallel lines in segments with the same ratio are concurrent.
Solution 4
We refer to the following diagram:

$\displaystyle \begin{align} MN\cap AC\cap BD=K&\,\Leftrightarrow\,\frac{MB}{MC}=\frac{ND}{NA}\\ &\,\Leftrightarrow\,\frac{BC+BF-FC}{FC+BC-BF}=\frac{AF+AD-FD}{AD+FD-AF}\\ &\,\Leftrightarrow\,\frac{BF-FC}{BC}=\frac{AF-FD}{AD}\\ &\,\Leftrightarrow\,\frac{BC}{AD}=\frac{BF-FC}{AF-FD}, \end{align}$
which is t rue because $BC\parallel AD\,$ implies that triangles $FBC\,$ and $FAD\,$ are similar so that
$\displaystyle \frac{BC}{AD}=\frac{BF}{AF}=\frac{FC}{FD}=\frac{BF-FC}{AF-FD}.$
P.S.
The external angle bisectors intersect in two additional points, $P\,$ and $S,\,$ besides the excenters (the centers of $\omega_1\,$ and $\omega_2.)\,$
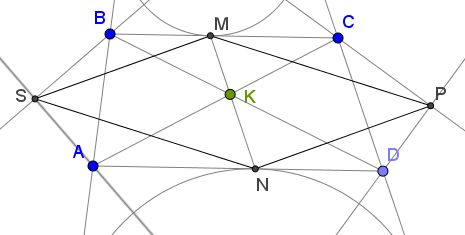
The quadrilateral $MSNP\,$ is a parallelogram.
P.P.S.
Acknowledgment
The problem has been posted at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group by Giannis Manikas. Solution 2 is by Amit Itagi; Solution 3 is by Kostas Theodoros Rekoumis (translated by Takis Chronopoulos; Solution 4 is by Vaggelis Stamatiadis. Giannis Manikas has mentioned that the problem that has been given in 2006 at the All-Russia Math Olympiad.
Thanos Kalogerakis has brought to our attention the presence of a parallelogram in the above configuration (P.S.)
Tran Quang Hung has added another twist (P.P.S.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573666
