Chasing Secant Angles
Problem
In quadrilateral $ABCD,\;$ $P\;$ is the intersection of the diagonals; $M\in BD,\;$ $N\in AC\;$ such that $PM=PN.\;$ In addition, $\angle BAC=\angle BDC.$
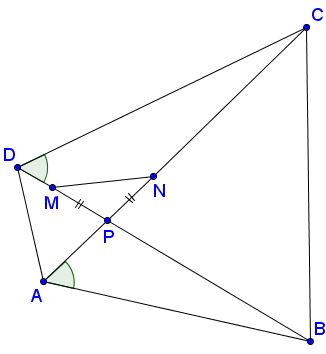
Prove that $MN$ makes equal angles with $AB\;$ and $CD.$
The problem is solved with angle chasing.
Solution 1
Because of $\angle BAC=\angle BDC,\;$ the quadrilateral is cyclic. Let $a,b,c,d\;$ denote the arcs of its circumcircle as shown below.
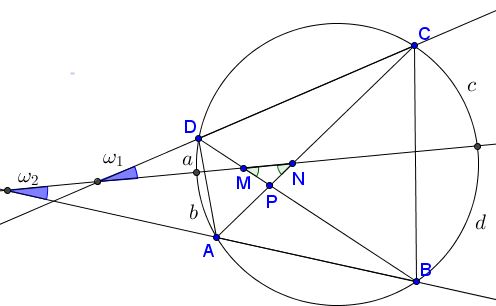
Then, from $PM=PN\;$ $\Delta MNP\;$ is isosceles, $\angle MNP=\angle NMP.\;$ For the secant angles we have
$2\angle MNP = b+c,\\ 2\angle NMP=a+d,$
implying $c-a=d-b.\;$ But for the angles $\omega_1\;$ and $\omega_2,\;$ (see the diagram)
$2\angle\omega_1 = c-a,\\ 2\angle\omega_2=d-b,$
making the two equal.
Solution 2
As before, we use the fact that the quadrilateral is cyclic. Assume, WLOG, that $PC\gt PD.\;$ Let $S\in PC\;$ satisfy $PS=PD.\;$ Let $DS\;$ intersect $(ABCD)\;$ the second time in $Q\;$ and $AB\;$ in $R.\;$ Note that $DS\parallel MN.$
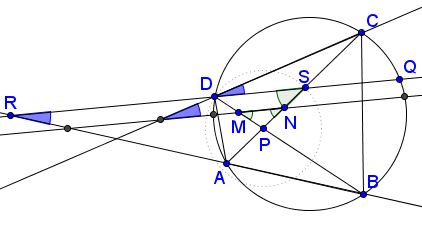
By the construction, $\angle SDP=\angle DSP=\angle NMP,\;$ and $2\angle CDQ=\overparen{CQ}.\;$ Further,
$\overparen{BQ}=2\angle SDP=2\angle DSP= \overparen{AD}+\overparen{CQ}.$
On the other hand, $2\angle QRB=\overparen{BQ}-\overparen{AD}.\;$ Thus, it follows that $\angle QRB=\angle CDQ.$
Solution 3
We'll prove a related statement:
Let $X$ be the intersection of the sidelines $AB\;$ and $CD\;$ of a cyclic quadrilateral $ABCD;\;$ let $P\;$ be the intersection of the diagonals. Assume the bisector of angle $AXD\;$ meets $BD\;$ in $U\;$ and $AC\;$ in $V.$

Then $PU=PV.$
Let the bisector meet the circle in $F\;$ and $G,\;$ as shown above. Then
$\overparen{CG}-\overparen{DF}=2\angle CXG=2\angle BXG=\overparen{BG}-\overparen{AF},$
meaning that
$2\angle UVP=\overparen{CG}+\overparen{AF}=\overparen{BG}+\overparen{DF}=2\angle VUP.$
Thus $\angle UVP=\angle VUP,\;$ making $\Delta UPV\;$ isosceles: $PU=PV.\;$ Now, any line parallel to $UV\;$ makes equal angles with $AB\;$ and $CD.$
Acknowledgment
The problem was posted by Daniel Dan at the Imad Zak Math Group and by Leo Giugiuc at the CutTheKnotMath facebook page. Solution 1 is by Daniel Dan. Solution 2 is by Leo Giugiuc and Dan Sitaru.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580757
