Problem 1 from the EGMO2017
What Is It About?
Problem
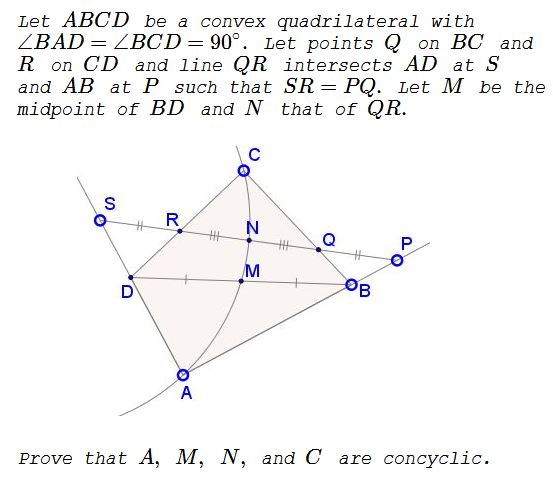
Solution 1
The main device for the solution is angle chasing and the main configuration to which the angle chasing will be applied is the right triangle:
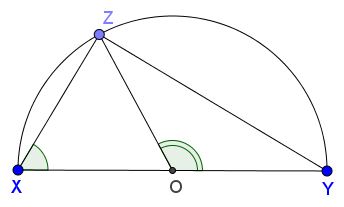
Since in any right triangle the circumcenter is the midpoint of the hypotenuse, $\angle YOZ=2\angle YXZ,\,$ as the central and inscribed angles subtended by the same arc.
To return to the problem, assume $\angle ADC\gt\angle ABC.\,$ (The case where $\angle ADC\lt\angle ABC\,$ is entirely analogous; in case $\angle ADC=\angle ABC\,$ $ABCD\,$ is a rectangle, the circle degenerates into a straight line and the four points $A,\,$ $M\,$ $N,\,$ and $C\,$ are collinear.)
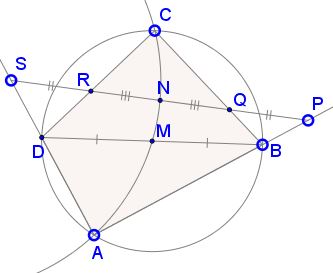
Now, in $\Delta ABD,\,$ $\angle AMD=2\angle ABD\,$ and, in $\Delta BCD,\,$ $\angle CMD=2\angle CBD,\,$ such that
$\angle AMC=2\angle ABC.$
In $\Delta PAS,\,$ $\angle ANS=2\angle APN\,$ and, in $\Delta QCR,\,$ $\angle CNR=2\angle CQR$ such that
$\begin{align}\angle ANC&=2(\angle APN+\angle CQR)\\ &=2(180^{\circ}-\angle PBQ)=2\angle ABC=\angle AMC. \end{align}$
So that, finally, $\angle ANC=\angle AMC,\,$ meaning they are inscribed into the same circle and, thus points $A,\,$ $M\,$ $N,\,$ and $C\,$ are indeed concyclic.
Solution 2
Let $\hat{x}$, $\hat{y}$, $\hat{u}$, and $\hat{v}$ be unit vectors along $\vec{AP}$, $\vec{AS}$, $\vec{CR}$ and $\vec{CQ}$, respectively. $(\hat{u},\hat{v})$ and $(\hat{x},\hat{y})$ are two fixed orthogonal systems and can thus be related by an orthogonal transformation:
$\displaystyle\begin{align} \hat{u}&= \cos\xi\hat{x}+\sin\xi\hat{y} \\ \hat{v}&= -\sin\xi\hat{x}+\cos\xi\hat{y}. \end{align}$
Here, $\xi$ is the angle between $\hat{x}$ and $\hat{u}$.
Let the radius of the circumcircles of $CRQ$ and $APS$ be $r$ and $R$, respectively. Let $\angle CNR = 2\alpha$ and $\angle ANS = 2\beta$. Thus,
$\displaystyle\begin{align} \vec{CR}&= 2r\sin\alpha\hat{u} \\ \vec{CQ}&= 2r\cos\alpha\hat{v} \\ \vec{CN}&= r\sin\alpha\hat{u}+r\cos\alpha\hat{v} \\ \vec{AS}&= 2R\sin\beta\hat{y} \\ \vec{AP}&= 2R\cos\beta\hat{x} \\ \vec{AN}&= R\cos\beta\hat{x}+R\sin\beta\hat{y} \end{align}$
and
$\displaystyle\begin{align} \vec{NS}&= \vec{AS}-\vec{AN}=-R\cos\beta\hat{x}+R\sin\beta\hat{y} \\ \vec{NR}&= \vec{CR}-\vec{CN}=r\sin\alpha\hat{u}-r\cos\alpha\hat{v} \\ &= (r\sin\alpha\cos\xi+r\cos\alpha\sin\xi)\hat{x} + (r\sin\alpha\sin\xi-r\cos\alpha\cos\xi)\hat{y} \\ &= r\sin(\alpha+\xi)\hat{x}-r\cos(\alpha+\xi)\hat{y} \end{align}$
$\vec{NR}$ and $\vec{NS}$ are parallel. Thus,
$\displaystyle\begin{align} \cos\beta\cos(\alpha+\xi)-\sin\beta\sin(\alpha+\xi)&= 0 \\ \cos(\alpha+\beta+\xi)&= 0 \end{align}$
Thus, $\alpha+\beta=(2K+1)\frac{\pi}{2}-\xi$ for integral $K$. The above analysis holds if $M$ is chosen as a special case of $N$. In this case, $R$ ans $S$ coalesce into $D$ and $Q$ and $P$ intp $B$. Note that as $N$ is continuously transformed into $M$, the integral value of $K$ has to remain fixed otherwise, $\angle CNA = 2(\alpha+\beta)$ will have to make step jumps of multiples of $\pi$. This also means that $\angle CNA = \angle CMA$. Thus, $CNMA$ are concyclic.
Acknowledgment
I am grateful to Vincent Pantaloni for bringing this problem (Problem 1 from the European Girls' Mathematical Olympiad 2017) to my attention over the twitter and to Vaggelis Stamatiadis for the solution (Solution 1) at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Solution 2 is by Amit Itagi
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581373
