Divide Triangle by Lines Parallel to Base
What Might This Be About?
Problem
Divide a triangle into $n$ pieces ($n\ge 1)$ of equal areas by lines parallel to the base.
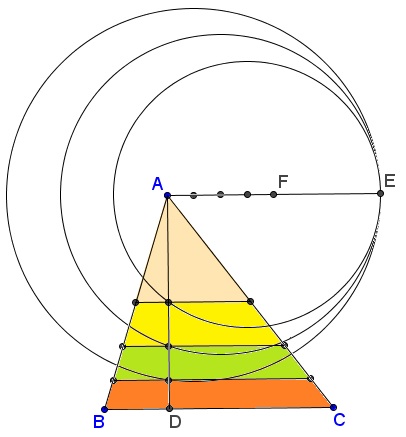
Solution
Let $ABC$ be a given triangle, with base $BC.$ Draw $AE,$ parallel and equal to $BC.$ Let $F$ be the middle point of $AE,$ and $X$ and arbitrary point on $AF.$
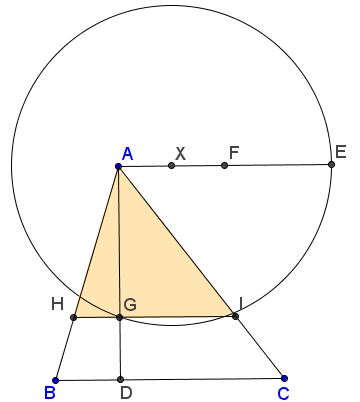
Draw circle $C(X,E)$ centered at $X$ and passing through $E.$ Let $G$ be the point of intersection of the circle with the altitude $AD,$ and $HI$ through $G$ parallel to $BC,$ with $H$ and $I$ on $AB$ and $AC,$ respectively. Then
$\displaystyle\frac{\mbox{Area}(\Delta AHI)}{\mbox{Area}(\Delta ABC)}=\frac{XF}{AF}.$
To see that it is so and without the loss of generality, let $AD=2$ and $XF=x.$ Draw $GX.$
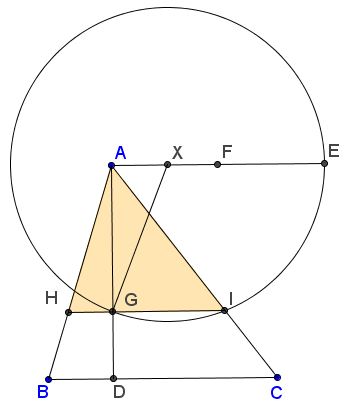
Then $AF=FE=1,$ $XG=XE=1+x,$ and $AX=1-x.$ In the right triangle $AXG,$ $AG^{2}+AX^{2}=GX^{2}.$ Thus
$AG^{2}=GX^{2}-AX^{2}=(1+x)^{2}-(1-x)^{2}=4x.$
But from $\displaystyle\frac{\mbox{Area}(\Delta AHI)}{\mbox{Area}(\Delta ABC)}=\frac{HI\cdot AG}{BC\cdot AD}$ and $\displaystyle\frac{AD}{AG}=\frac{BC}{HI}$ we obtain $\displaystyle\frac{\mbox{Area}(\Delta AHI)}{\mbox{Area}(\Delta ABC)}=\frac{AG^2}{AD^2}=\frac{4x}{4}=x.$
Acknowledgment
The ingenious construction discussed above is due to Jean David, Gagny (France) whose post at google+ has taken me by surprise.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73517414
