Dimensionless Inequality in the Euclidean Plane
Problem
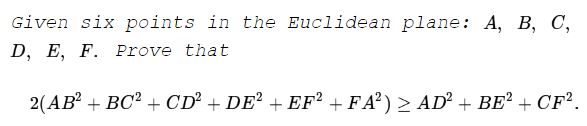
Proof 1
Let the points have coordinates $(x_k,y_k),\,$ $k=1,\ldots,6.\,$ Setting $(x_7,y_7)=(x_1,y_1),\,$ the required inequality becomes
$\displaystyle 2\left(\sum_{k=1}^6\left[(x_{k+1}-x_k)^2+(y_{k+1}-y_k)^2\right]\right)\ge\sum_{k=1}^3\left[(x_{k+3}-x_k)^2+(y_{k+3}-y_k)^2\right].$
This will be proved if we manage to show that
$\displaystyle 2\left(\sum_{k=1}^6(x_{k+1}-x_k)^2\right)\ge\sum_{k=1}^3(x_{k+3}-x_k)^2,\\ \displaystyle 2\left(\sum_{k=1}^6(y_{k+1}-y_k)^2\right)\ge\sum_{k=1}^3(y_{k+3}-y_k)^2.$
Obviously, suffice it to prove just one of these inequalities as the difference between the two is exclusively notational. Remarkably, this would mean that the problem could have been posed in any Euclidean space $\mathbb{R}^n,\,$ $n\ge 1,\,$ and not just the Euclidean plane.
Thus introduce $a_k=x_{k+1}-x_k,\,$ $k=1,\ldots,6.\,$ The first inequality then reduces to
$\displaystyle 2\left(\sum_{k=1}^6a_k^2\right)\ge\sum_{k=1}^3(a_{k+2}+a_{k+1}+a_{k})^2.$
Note that by the definition, $\displaystyle\sum_{k=1}^6a_k=0.\,$ With this constraint, the above inequality is equivalent to
$\displaystyle 2\left(\sum_{k=1}^5a_k^2\right)+2\left(\sum_{k=1}^5a_k\right)^2\ge\sum_{k=1}^3(a_{k+2}+a_{k+1}+a_{k})^2.$
The latter can be transformed into
$\displaystyle \left(\sum_{k=1}^5a_k\right)^2 + (a_1+a_3+a_5)^2 + (a_1+a_4)^2+(a_2+a_5)^2\ge 0$
which is of course true.
Proof 2
Let's define $AB=\overrightarrow{b},\,$ $AC=\overrightarrow{c},\,$ $AD=\overrightarrow{d},\,$ $AE=\overrightarrow{e},\,$ $AF=\overrightarrow{f}.\,$ Then
$\displaystyle\text{LHS - RHS}=3\left|\overrightarrow{b}-\frac{2\overrightarrow{c}-\overrightarrow{e}}{3}\right|^2+3\left|\overrightarrow{d}-\frac{2}{3}(\overrightarrow{c}+\overrightarrow{e})\right|^2+3\left|\overrightarrow{f}+\frac{\overrightarrow{c}-2\overrightarrow{e}}{3}\right|^2.$
Acknowledgment
The problem from the Romanian Mathematical Magazine has been kindly shared at the CutTheKnotMath facebook page by Dan Sitaru, along with the beautiful solution by Ioan Serdean. Proof 2 is by Kunihiko Chikaya.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578552
