An Identity in Bicentric Isosceles Trapezoid
Source
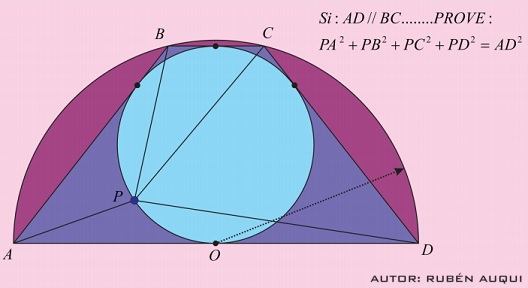
Problem
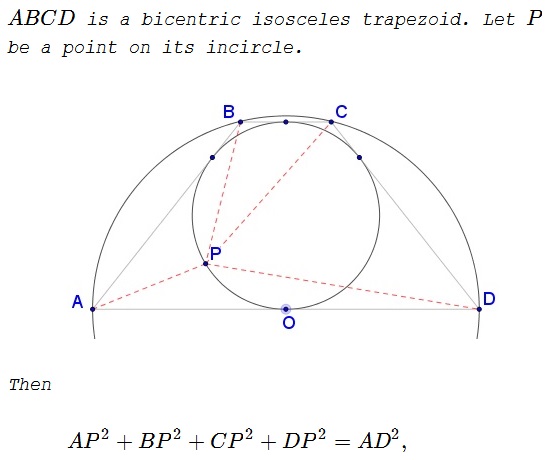
Solution 1
Let $A=(-1,0),$ $D=(1,0),$ $C=(\cos 2t,\sin 2t),$ $B=(-\cos 2t,\sin 2t),$ with $\displaystyle t\in\left(0,\frac{\pi}{4}\right).$ We have
$AD=2,$ $BC=2\cos 2t,$ $AB=CD=2\sin t.$
Since $AD+BC=AB+CD,$ we obtain
$1+\cos 2t=2\sin t,$
from which $\displaystyle \sin t=\frac{\sqrt{5}-1}{2},$ $\cos 2t=\sqrt{5}-2,$ and $\sin 2t=2\sqrt{\sqrt{5}-2}.$ So, if $r=\sqrt{\sqrt{5}-2},$ then $C=(r^2,2r)$ and $D=(r^2,-2r).$ The incenter is at $I=(0,r)$ and $r$ is the inradius.
Thus, $P=r\cos u,R+r\sin u),$ with $U$ a real number. We get
$BP^2+CP^2=2r^2(r^2+2-2\sin u),\\ AP^2+DP^2=4r^2+2+4r^2\sin u,$
implying
$\begin{align} AP^2+BP^2+CP^2+DP^2 &= 2r^4+8r^2+2\\ &=4=AD^2. \end{align}$
Solution 2
Let $OA=R$ and the radius of the incircle be $r$. Let $Q$ be the center of the incircle. Let the positive $X$ and $Y$ axes be along $OD$ and $OQ$, respectively. Thus,
$\displaystyle \begin{align} &\vec{OD}=R\hat{x},~\vec{OA}=-R\hat{x} \\ &\vec{OC}=\sqrt{R^2-4r^2}\hat{x}+2r\hat{y},~\vec{OB}=-\sqrt{R^2-4r^2}\hat{x}+2r\hat{y} \\ &\vec{QP}=r\cos\phi\hat{x}+r\sin\phi\hat{y},~\vec{OP}=\vec{OQ}+\vec{QP} =r\cos\phi\hat{x}+(r+r\sin\phi)\hat{y}. \end{align}$
$\phi$ is the polar angle of $\vec{QP}$ with origin at $Q$.
$\displaystyle \begin{align} &PA^2+PB^2+PC^2+PD^2 \\ &=|\vec{OA}-\vec{OP}|^2 +|\vec{OB}-\vec{OP}|^2 +|\vec{OC}-\vec{OP}|^2 +|\vec{OD}-\vec{OP}|^2 \\ &=|\vec{OA}|^2+|\vec{OB}|^2+|\vec{OC}|^2+|\vec{OD}|^2 +4|\vec{OP}|^2-2(\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD})\cdot\vec{OP} \\ &=[2R^2+2(R^2-4r^2)+8r^2]+4[2r^2+2r^2\sin\phi] -2(4r)(r\sin\phi+r)=4R^2=AD^2. \end{align}$
Acknowledgment
This problem by Ruben Auqui (Dario) was kindly communicated to me by Leo Giugiuc, along with a solution of his. The problem was originally posted at the Peru Geometrico facebook group. Solution 2 is by Amit Itagi. Additional solutions can be found at the link.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581504
